Modal Characteristics and Lateral Load İncrement Determination (5B.1.1)
Modal Characteristics, Modal Additive Multiplier, Base Shear Modal Effective Mass and Mode Shape given in TDY APPENDIX 4B are calculated automatically.
ICONS
a first (X, k) = (X) seismic line to kth pushing step in the first mode of modal single degree of freedom system modal pseudo-acceleration [m / s2]
m i = i 'th times the total mass
m ix1 ( X,1) = (X)ith floor modal effective mass calculated accordingto the constant mode shape determined in the first thrust step in the x-axis direction and never changed during the thrustcalculation[t]
m tx1 (X,1) = ( X) fixed mode shape for the earthquake direction determined in the first thrust step in the x-axis direction and never changed during the thrust calculation
'ne calculated by base shear modal effective mass [t]
m iy1 (X, 1) = (X) earthquake direction of the y-axis direction of the first propulsion determined at step and push account never changed during the fixed mode shape ' what i'th calculated floor modal effective mass [t]
m iθ1 (X,1) = ith floor modal effective mass moment of inertia calculated according to the constant mode shape determined in the first thrust step around the z axis for the earthquake direction and never changed during the thrust calculation [tm2]
Δa 1 (X,k) = (X) modal pseudo-acceleration increment of the first mode modal single degree of freedom system at the kth thrust step for the earthquake direction [m/s 2 ]
Δf ix1 (X,k) = the kth for the (X) earthquake direction Earthquake load increase acting in the x-axis direction at the i th floor in the push step [kN]
Δf iy1 (X,k) = (X) earthquake load increase acting in the y axis direction at the i th floor at the kth push step for the earthquake direction [kN]
Δf iθ1 (X,k) = Increment of earthquake load acting in the z-axis direction at the i'th floor at the k'th push step for the (X) earthquake direction [kN]
Φix1 (1) =constant mode shapein the x direction of theconstant mode shapedetermined in the first push step at the i'th floor and never changed during the push calculation
Φ iy1 (1) = theconstant mode shapedetermined in the first push step at the i'th floor and never changed during the push calculationAmplitude of ' in the y direction
Φ iθ1 (1) =Rotation amplitude about the z-axis of theconstant mode shapedetermined in the first thrust step at the i'th floor and never changed during the thrust calculation
Γ 1 (X,1) = (X) first for the earthquake direction determined in the push step and never changed during the push calculation.modal contribution factor calculated according to fixed mode shape
Constant Single Mode Pushover Analysis Method, earthquake load increments acting on the floors at each push step in the direction of the considered earthquake , non-linear increment under non- earthquake loadings, determined in the first step after the static calculation (0 th step) and never changed during the thrust calculation. defined in proportion to the fixed mode shape . As a result of the thrust analysis, the thrust curve whose coordinates are the base shear force-peak displacement is obtained. Then, by applying coordinate transformation to this curve , a modal capacitance diagram whose coordinates are modal displacement-modal pseudo-acceleration is obtained. As a result of the performance point obtained using the fashion capacity diagram , the plastic deformations and internal forces at this performance point are compared with the limit values to determine the building performance.
As stated in TDY Appendix 5B.1.1 , in the Constant Single Mode Pushing Method , internal forces and deformations, which take into account the second-order effects of non-earthquake loadings, are taken into account as the initial value (0 th step). K in the earthquake direction taken into consideration lactide floors of the seismic load increment in the pushing step, earthquake off after the first step of the installation modal analysis methods are calculated by using the mode shape and fold modal effective mass in terms of Equation 5B.1 expressed by.
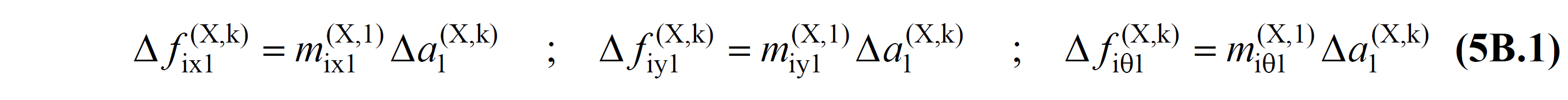
Here, the terms Δf ix1 (X,k) , Δf iy1 (X,k) and Δf iθ1 (X,k) are the earthquake load increments acting on the floors at the kth push step for the earthquake direction ( X ) considered. The terms m ix1 (X,1) , m ix1 (X,1) and m iθ1 (X,1) are the first mode (dominant mode) equivalent of the floor effective masses calculated in the first step and are calculated using Equation 5B.2 .
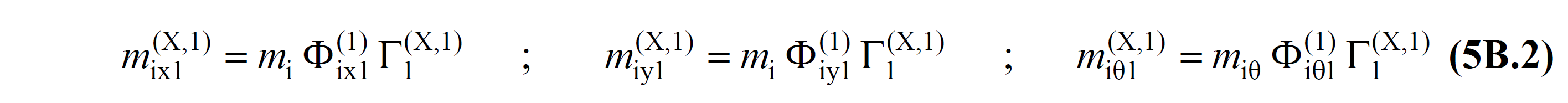
In Equation 5B.2 , the terms Φ ix1 (1) , Φ iy1 (1) and Φ iθ1 (1) are the first (dominant) mode shape obtained by making the modal analysis of the deformed system in the initial step, considering the second-order effects consisting of non-earthquake loadings . This mode shape is expressed as the corresponding x, y, z axes, respectively. In the same equation , the value of Γ 1 (X,1) is the modal contribution factor obtained as a result of the modal analysis performed in the initial step .
Mass Definition at Joints (5.4.6)
Calculation of Combined Response Parameters and Scaling Design Values of Combined Response (4.8.2.1)
The unknown magnitude at the k th thrust step defined between two successive hinge joint formations is the modal pseudo acceleration increment Δa 1 (X,k) included in Eq.(5B.1) of the modal single degree of freedom system belonging to the first mode , and detailed explanation is available at Determination of Modal Pseudo-Acceleration, Modal Displacement Increment (5B.1.2 , 5B.1.3).
