Composite Beam Design
Symbols
Asa = Cross-sectional area of shear stud, in.2 (mm2)
Ec = Modulus of elasticity of Concrete, ksi (MPa)
Fu = Specified minimum tensile strength of a shear stud, ksi (MPa)
As = Area of steel cross-section, in.2 (mm2)
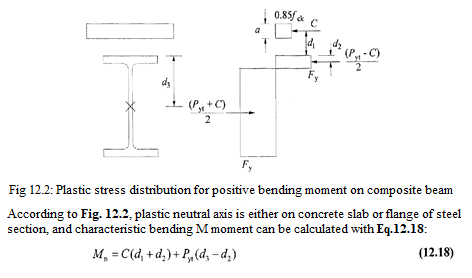
d3 = Distance from the resultant steel tension force for full section tension yield to the top of the steel, in.
ILB = Lower bound moment of inertia, in.4 (mm4)
Is = Moment of inertia for the structural steel section, in.4 (mm4)
ΣQn = Sum of the nominal strengths of shear studs between the point of the maximum positive moment and the point of zero moments to either side, kips (kN)
Ac = Area of concrete slab within effective width, in.2 (mm2)
Fy = Specified minimum yield stress of steel, ksi (MPa)
fc′ =Specified compressive strength of concrete, ksi (MPa)
d1 = Distance from the centroid of the compression force C in the concrete to the top of the steel section, in. (mm)
d2 = Distance from the centroid of the compression force in the steel section to the top of the steel section, in. (mm). For the case of no compression in the steel section, d2 = 0.
Bending Moment Strength
Effective Width of Concrete Slab beff
As defined in Section 21.4.1.1 of ÇYTHYEDY 2018, composite slab effective width is determined by the sum of effective widths defined on both sides of the beam. Each effective width is determined less than the distances defined below:
1/8 of the beam span
Half of the distance from the axis of the beam cross-section to the axis of the adjacent beam cross-section
The distance from the axis of the beam cross-section to the free edge of the reinforced concrete slab
Plastic Stress Distribution
Characteristic bending moment strength Mn is determined according to ÇYTHYEDY 12.4.2.1 and AISC 360-10 I3.2a by plastic stress distribution method in the composite section.
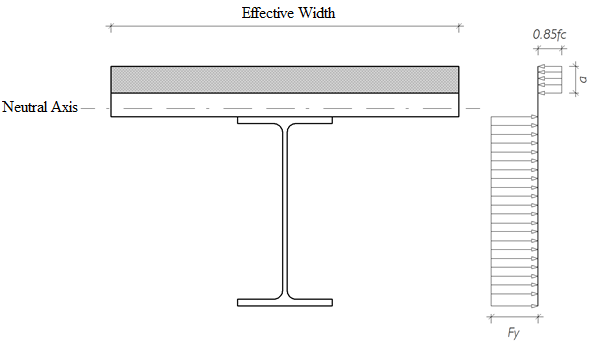
Compressive Strength of Reinforced Concrete Slab
The value of compressive force C in reinforced concrete slab should be calculated by considering 3 conditions defined in AISC 360-10 and ÇYTHYEDY:
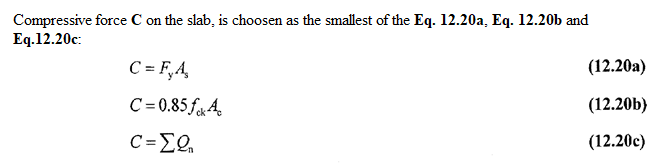
Shear Strength of Studs
The characteristic shear strength of studs embedded in concrete is calculated according to AISC and ÇYTHYEDY:

Composite Ratio, PCC
It is the ratio of the sum of the shear strengths of the studs ΣQn between the points where the positive bending moment is maximum and zero to the compressive force in the reinforced concrete slab, C.

Depth of Concrete Compression Block
The depth of the concrete compression block is calculated according to AISC and ÇYTHYEDY with the following formula:

Design Bending Moment Strength
Design bending moment strength for composite beams should be calculated according to ASD (GKT) and LRFD (YDKT):
Mc = Mn / Ω for ASD (GKT) and Mc = ϕMn for LRFD (YDKT)
Computation on Construction Phase
Loads that act during the construction phase, must be taken into account in the design. When temporary supports are not used during the construction phase, since all loads will be carried only by the steel cross-section, the bending moment strength is determined should be considered without the composite cross-section.
Deflection and Moment of Inertia
Deflection is calculated in AISC 360-10 using the lower bound moment of inertia value according to the formula C-I3-1.
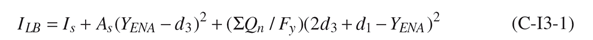

Next Topic
