Slab Stress Controls
ICONS
D = Strength Excess Coefficient
f cd = Design compressive strength of concrete
f ctd = Design tensile strength of concrete
f yd = Design yield strength of reinforcement
f ck = Characteristic cylinder compressive strength of concrete
ρ = ratio of reinforcement remaining from the required for flexural strength
τ r = In- plane shear stress strength
TBDY Article 7.11.3 - In -plane axial and shear stresses in floors of buildings with and without beams shall be calculated with the acceptance of elastic diaphragm. The Strength Excess Coefficient D will be applied to the in-plane average tensile, compression and shear stresses that occur under the effect of earthquakes in the floors of these buildings. In case the tensile stress value occurring in the slab plane is greater than f ctd , the in-plane tensile stress value will not exceed the limit ρf yd , with the remaining reinforcement ratio being ρ from the bending strength of the slab . In cases where this condition is not fulfilled, the reinforcement shortage will be supplemented with additional reinforcement in-plane. Compressive stress occurring in the floor plane 0.85f cdwill not exceed the limit. The horizontal shear stresses in the floor plane in both directions will not exceed the limit given by Equation (7.25) .
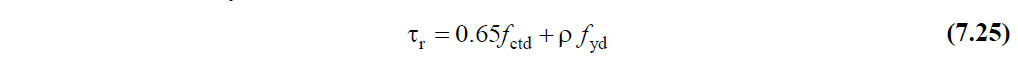
In this calculation, ρ is the ratio of the slab reinforcement that is left over from what is required for bending strength and will be placed in a parallel direction to the shear stress. The shear stress occurring in the plane shall not exceed 0.65 (f ck ) 1/2 limit.
The in-plane shear stresses that occur between the floor and the curtain will not exceed the in-plane shear friction strength at these sections. The shear friction strength shall be calculated in terms of stress by Equation (7.26) with the remaining slab reinforcement ratio ρ, which is stuck to the wall and whose clamping length is sufficient and required for bending strength .
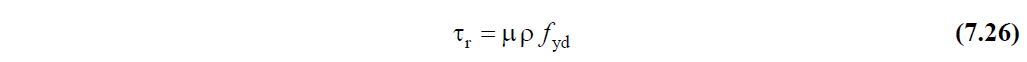
The value of μ = 1.0 will be used for the shear friction coefficient in casting joints.
