Punching Shear Design per ACI 318-19 with ideCAD

How does ideCAD calculate the punching shear required and design strength according to ACI 318-19?

• Slab punching shear is checked automatically in accordance with ACI 318 - Chapter 8.

• Punching shear reinforcement is defined by user.

Download ideCAD and try how punching Shear Design per ACI 318-19 Works.

Notation

A_g = gross area of the concrete section, in²
A_s = area of non prestressed longitudinal tension reinforcement, in²
b_o = perimeter of critical section for two-way shear in slabs and footings, in.
b_slab = effective slab width, in.
b₁ = dimension of the critical section b_o measured in the direction of the span for which moments are determined, in.
b₂ = dimension of the critical section b_o measured in the direction perpendicular to b₁, in.
d = distance from extreme compression fiber to centroid of longitudinal tension reinforcement, in.
E_c = modulus of elasticity of concrete, psi
E_s = modulus of elasticity of reinforcement, psi
√f_c‘ = square root of specified compressive strength of concrete, psi
f_c^' = specified compressive strength of concrete, psi
f_y = specified yield strength for nonprestressed reinforcement, psi
J_c = property of assumed critical section analogous to polar moment of inertia
M_sc = factored slab moment that is resisted by the column at a joint, in.-lb
v_c = stress corresponding to nominal two-way shear strength provided by concrete, psi
v_uv = factored shear stress on the slab critical section for two-way action, from the controlling load combination, without moment transfer, psi
α_s = constant used to calculate V_c in slabs and footings
ϕ = strength reduction factor
λ = modification factor to reflect the reduced mechanical properties of lightweight concrete relative to normalweight concrete of the same compressive strength
λ_s = factor used to modify shear strength based on the effects of member depth, commonly referred to as the size effect factor
ε_t = net tensile strain in extreme layer of longitudinal tension reinforcement at nominal strength, excluding strains due to effective prestress, creep, shrinkage, and temperature
ε_ty = value of net tensile strain in the extreme layer of longitudinal tension reinforcement used to define a compression-controlled section
γ_f = factor used to determine the fraction of M_sc transferred by slab flexure at slab-column connections
γ_v = factor used to determine the fraction of M_sc transferred by eccentricity of shear at slab-column connections

Factored Slab Moment Resisted by the Columns

According to ACI 8.4.2.2.1, if gravity, wind, earthquake, or other loads cause a moment at the slab-column joint, a fraction of M_sc , the factored slab moment resisted by the column at a joint, should be transferred by flexure in accordance with ACI 8.4.2.2.2 through ACI 8.4.2.2.5.

According to ACI 8.4.2.2.2, the fraction of unbalanced factored slab moment resisted by the column, γ_fM_sc , is assumed to be transferred by flexure. γ_f is calculated in accordance with ACI Eq.(8.4.2.2.2);

The fraction of unbalanced moment transferred by the eccentricity of shear is taken to be γ_vM_sc and the factor γ_v equals 1- γ_f. (γ_v=1- γ_f )

According to ACI 8.4.2.2.4, for nonprestressed slab systems without beams, where the limitations on v_uv and ε_t in ACI Table 8.4.2.2.4 are satisfied, γ_f can be increased to maximum modified values provided in ACI Table 8.4.2.2.4. The calculation of two-way shear strength provided by concrete without shear reinforcement v_c is explained in Two-Way Shear Strength per ACI 318-19 with ideCAD title.

Critical Section

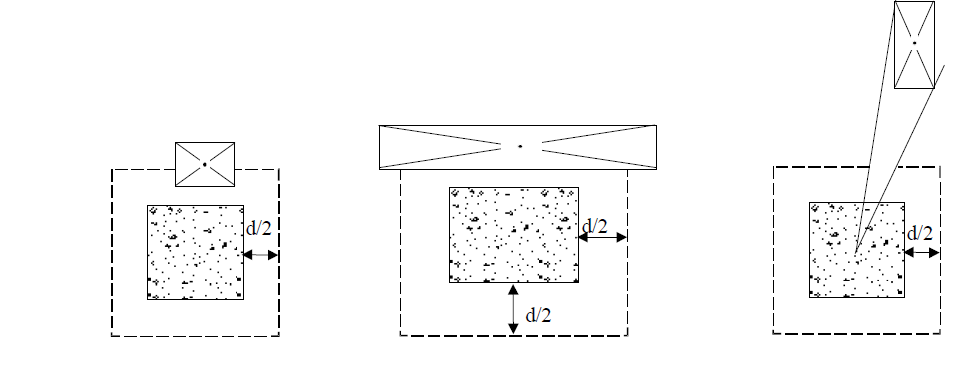
According to ACI 22.6.4.1, for two-way shear, critical sections should be located so that perimeter b_o is a minimum but need not be closer than d/2 to the two cases given below;

1. Edges or corners of columns, concentrated loads, or reaction areas

2. Changes in slab or footing thickness, such as edges of capitals, drop panels, or shear caps

According to ACI 22.6.4.1.1, concentrated loads, or reaction areas, critical sections for two-way shear in accordance with ACI 22.6.4.1 (case 1 and case 2) can be defined assuming straight sides for square or rectangular columns.

According to ACI 22.6.4.1.2, critical sections for two-way shear in accordance with ACI 22.6.4.1 (case 1 and case 2) can be defined assuming a square column of equivalent area for a circular or regular polygon-shaped column.

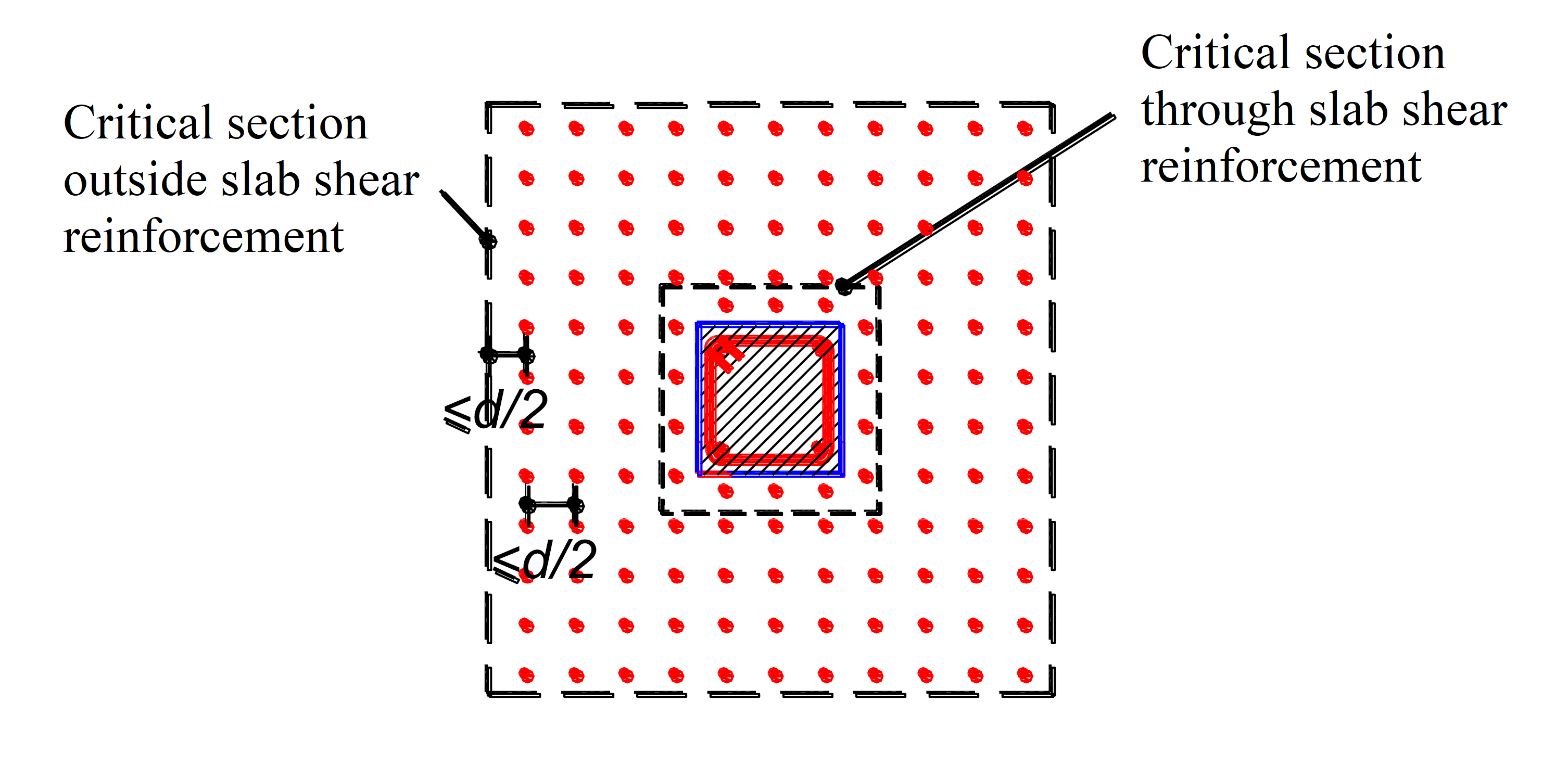
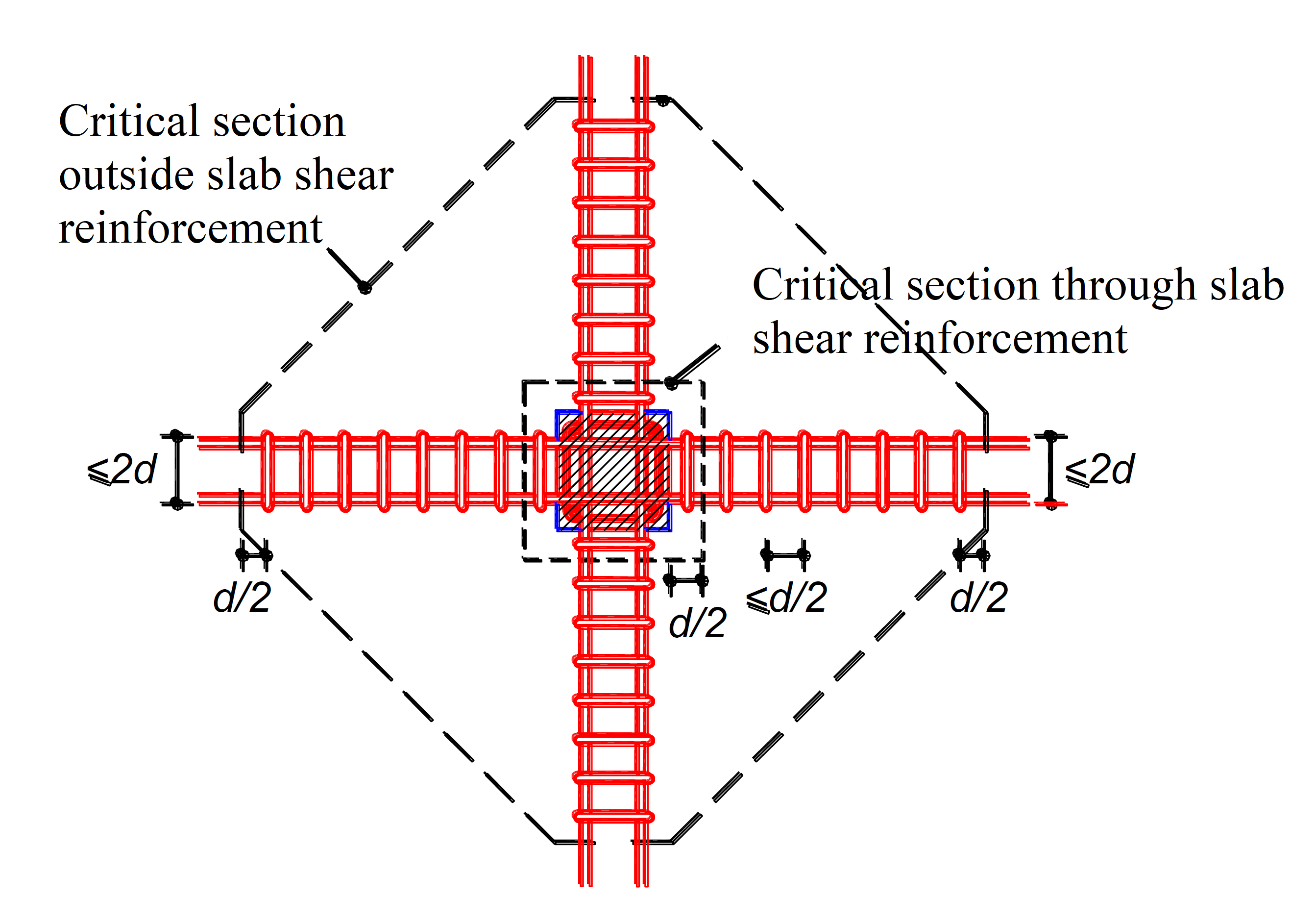
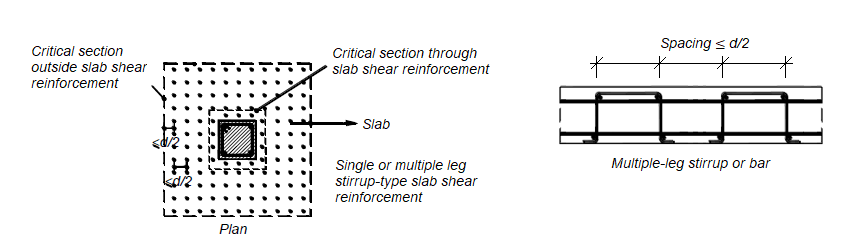
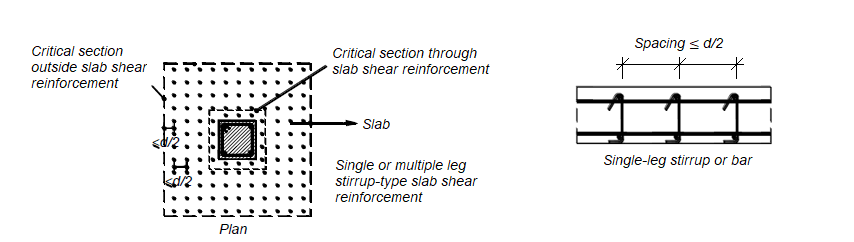
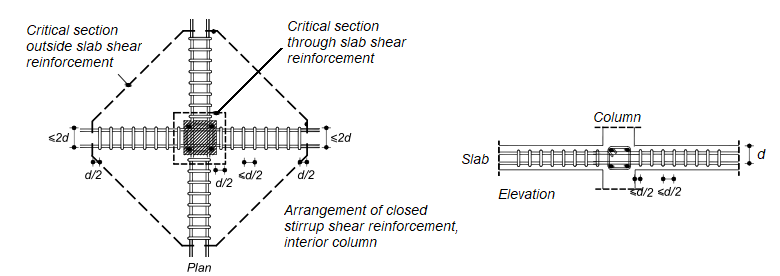
According to ACI 22.6.4.2, for two-way members with single (or multi) leg stirrup or headed stud shear reinforcement, one more critical section with perimeter b_o located d/2 beyond the point where shear reinforcement is discontinued. The shape of this critical section should be a polygon selected to minimize b_o.

The value of b_o is shown in the figure below.

According to ACI 22.6.4.3, If there is an opening located closer than 4h from the periphery of a column, concentrated load, or reaction area, the portion of b_o enclosed by straight lines projecting from the centroid of the column, concentrated load or reaction area and tangent to the boundaries of the opening should be considered ineffective.

Factored Two-way Shear Stress Due to Shear and Factored Slab Moment Resisted by the Column

According to ACI 8.4.4.2.1, for punching shear with factored slab moment resisted by the column, factored shear stress v_u should be calculated at critical sections. Factored shear stress v_u corresponds to combinations of v_uv and γ_vM_sc.

According to ACI 8.4.4.2.2, γ_vM_sc is the fraction of unbalanced moment transferred by eccentricity of shear. The fraction of M_sc should be applied at the centroid of the critical section. γ_v is taken as specified in ACI Eq. (8.4.4.2.2);

According to ACI 8.4.4.2.3, the factored shear stress caused by γ_vM_sc is assumed to vary linearly about the centroid of the critical section.

The stress distribution is assumed for the interior and edge columns, as illustrated in ACI Fig. R8.4.4.2.3. For the interior column, the perimeter of the critical section equals 2(c₁+d+c₂+d). For the edge column, the perimeter of the critical section equals 2(c₁+d) + (c₂+d).

The factored shear stress v_uv and factored slab moment resisted by the column M_sc are determined at the centroidal axis c-c of the critical section. According to the stress distribution shown in ACI Fig. R8.4.4.2.3. The maximum factored punching shear stress is calculated from;

For an interior column, the property of the assumed critical section analogous to the polar moment of inertia, J_c, is calculated by:

Punching shear stress with biaxial bending can similarly be applied for two perpendicular moment directions. For the interior column, punching shear stresses v_u,1 and v_u,2 is calculated as follows;

For the interior column, polar moment of inertia values, J_c,1 and J_c,2 are calculated along the respective axes c₁ and c₂. v_uv means factored shear stress on the slab critical section for two-way action, from the controlling load combination, without moment transfer. v_uv calculated by dividing the axial force in the column by the critical section area [ v_uv = V / 2d(c₁+d+c₂+d) ]

Minimum flexural reinforcement in nonprestressed slabs

A minimum area of flexural reinforcement is satisfied near the slab's tension face in the span's direction.

A_s,min=0.0018A_g

According to ACI 8.6.1.2, if v_uv > 2ϕλ_sλ√f_c‘ on the critical section for two-way shear surrounding a column, concentrated load, or reaction area, A_s,min, provided over the width b_slab, shall satisfy ACI Eq. (8.6.1.2)

α_s and λ_s is given in Two-Way Shear Strength per ACI 318-19 with ideCAD title.

Shear Reinforcement - Stirrups

Single-leg, simple-U, multiple-U, and closed stirrups are used as shear reinforcement. Stirrup anchorage and geometry are determined with ACI 25.7.1. Detailed information: Stirrups per ACI 318-19 with ideCAD.
If stirrups are provided, location and spacing are determined with ACI Table 8.7.6.3.

The shear reinforcement engages longitudinal reinforcement at both the top and bottom of the slab, as shown for typical details in ACI Fig. R8.7.6(a) to (c). The shear reinforcement should be symmetrical
about the centroid of the critical section shown in ACI Fig. R8.7.6(d). Spacing limits defined in ACI 8.7.6.3 are shown below.

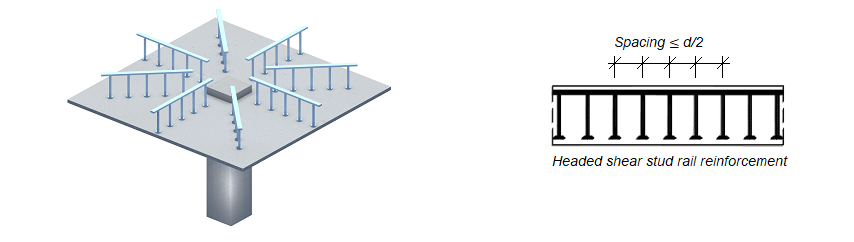
Shear Reinforcement - Headed Studs

According to ACI 8.7.7.1.1, the overall height of the shear stud assembly should be at least the thickness of the slab minus the sum of all given values below;

• concrete cover on the top flexural reinforcement

• concrete cover on the base rail

• One-half the bar diameter of the flexural tension reinforcement

According to ACI 8.7.7.1.2, Headed shear stud reinforcement location and spacing should be in accordance with ACI Table 8.7.7.1.2.

Related Topics

• One-Way Slab Design per ACI 318-19 §7

• Two-Way Slab Design per ACI 318-19 §8