Determination of Modal Pseudo-Acceleration, Modal Displacement Increment (5B.2.3 , 5B.2.4)
Modal Pseudo-Acceleration and Modal Displacements are calculated automatically at each push step.
ICONS
a 1 (X,k) = modal pseudo-acceleration of the first mode modal single degree of freedom system at the kth push step for the earthquake direction [m/s 2 ]
d 1 (X,k) = (X) modal displacement of the modal single degree of freedom system belonging to the first mode at the kth push step for the earthquake direction [m]
u ix1 (X,k) = (X) calculated in the x-axis direction at the i th floor at the kth push step for the earthquake direction displacement [m]
Δa 1 (X,k) = modal pseudo-acceleration increment [m/s 2 ] of the first mode modal single degree -of- freedom system at the kth push step for the earthquake direction (X)
Δd1 (X, k) = (X) k earthquake directions' of the first mode in th thrust step modal single degree of freedom system 's modal displacement of [m]
Δf ix1 (X, k) = (X) k earthquake directions' the pushing step Inc. i 'acting in accordance with the fifth floor in the x-axis seismic load increment [kN]
Δf iy1 (X, k) = (X) k earthquake direction of the' th thrust step i 'th floor acting in line with the y-axis seismic load increment [kN]
Δf iθ1 (X,k) = earthquake load increase acting in the z-axis direction at the i'th floor at the kth push step for the (X) earthquake direction[kN]
Δu ix1 (X,k) = Displacement increment calculated in the x-axis direction at the i'th floor at the kth push step for the (X) earthquake direction [m]
Δu iy1 (X,k) = (X) k for the earthquake direction Displacement increment calculated in the y-axis direction [m]
Δu iθ1 (X,k) = (X) at the i th floor at the th thrust step, the displacement increment calculated in the z axis direction at the i th floor at the kth thrust step for the earthquake direction [m]
Φ ix1 (k) = x-direction amplitude of the variable mode shape , which is renewed with free vibration calculation at each kth thrust step at the i'th floor
Φ iy1 (k) = The amplitude of the variable mode shape in the y direction, which is renewed with the free vibration calculation at each kth pushing step at the i'th floor
Φ iθ1 (k) = The variable mode shape is renewed with the free vibration calculation at each kth pushing step at the i'th floor The amplitude of
Γ in the z direction hesap 1 (X,k) = the modal contribution factor calculated according to the variable mode shape , which is renewed by the free vibration calculation at each k th thrust step for the earthquake direction ω 1 (k) = For each k The first mode natural angular frequency [rad/s] found from the free vibration calculation renewed in the th thrust step
Earthquake load increments calculated for each k th thrust step in an earthquake direction (X) considered in TDY Equation 5B.7 , Δf ix1 (X,k) , Δf iy1 (X,k) and Δf iθ1 (X,k) ) , the storey displacement increments Δu ix1 (X,k) , Δu iy1 (X,k) and Δu iθ1 (X,k) TBDY are obtained by Equation 5B.9 .
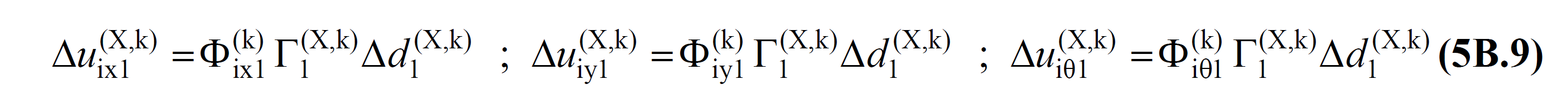
In this equation, expressed as a dimensionless one (X, k) , the term of spectral displacement of the increment are expressed. The values of Φ ix1 (k) , Φ iy1 (k) and Φ iθ1 (k) show that the dominant mode shape calculated as a result of the modal analysis made by taking into account the stiffness change caused by the plastic hinges at each k th thrust step in the considered (X) earthquake direction is the amplitude in the x, y, z axes, respectively. Γ 1 (X,k) It is the modal contribution factor calculated as a result of the modal analysis, taking into account the stiffness change caused by the plastic hinges at each kth thrust step, in the direction of the earthquake (X), whose value is taken into account .
Equation 5B.7 which is located k 'th thrust of step modal so-called acceleration increment, Δ A 1 (X, k) , with the modal displacement increments expressed as a dimensionless one (X, k) , the linear relationship stepwise between TDY equation 5B.10 at given.
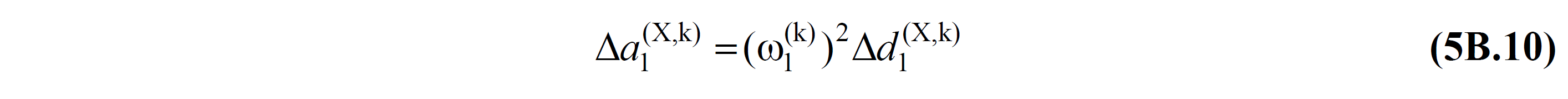
In this equation, ω is the natural angular frequency of the first mode (dominant mode) calculated as a result of the modal analysis performed at each kth push step of the 1 (k) carrier system .
According to TDY 5B.2.4 , the modal pseudo acceleration increment Δa 1 (X,k) of the first mode of the modal single degree-of-freedom system in Equation 5B.7 , as unknown magnitude, at the k th thrust step defined between two successive hinge formations. ) can be obtained. In this case, the calculation based on the force is made. However, the modal displacement increment Δd 1 (X,k) in Equation 5B.9 can be taken as an unknown quantity instead, to allow direct calculation of internal forces . In this case, calculation based on displacement is made. Variable as unknown magnitude in Unimodal Repulsion Analysis modal displacement increment Δd 1 (X,k) is taken and calculation based on displacement is made.
Modal displacement increment Δd 1 (X,k) is calculated from the yield conditions of the plastic hinge according to TDY 5B.2.4 . This increment is used to determine the iteration level.
After calculating the modal displacement increments Δd 1 (X,k) and the earthquake load increments, Δf ix1 (X,k) , Δf iy1 (X,k) and Δf iθ1 (X,k) , the modal capacity diagram is obtained directly. Then the impulse curve can be obtained by transforming the modal capacitance diagram. Pushover Curve and Modal Capacity Curve (5B.2.5 , 5B.2.6)
