15.5.4.5
The plastic rotation demand is calculated with the yield rotation calculated using the displaced axis rotation and the moment-curvature analysis when performing the linear performance analysis.
The element is automatically calculated according to the plastic rotation demand θ p Equation (15A.2) .
ICONS
E = Concrete modulus of elasticity
h = Section height
I = Moment of inertia
L p = Plastic hinge length
l c = Element net opening
M y = Effective yield moment
M yi = Effective yield momentat i end
M yj = Effective yield moment at j end
Δ = Element translation between nodes
ϕ y = Flow curvature
ϕ t = Total curvature
θ p =Plastic rotation demand
θ i = i joint rotation
θ j = j node rotation
θ y = flow rotation
θ yi = flow rotation at end i
θ yj = flow rotation at end j
θ k = displaced axis rotation
θ ki = displaced axis rotation at end i
Evaluation of existing buildings and design according to Strain (ŞGDT) determining the seismic performance of the linear approximation calculation method used plastic rotation element lead θ p Eq. (15A.2) from being calculated.
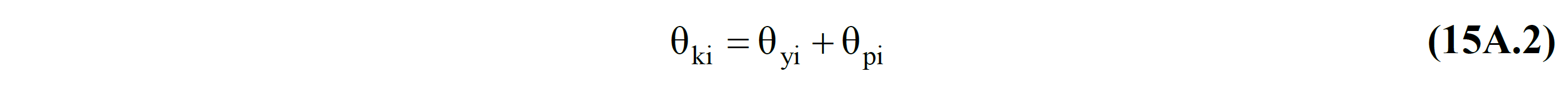
In the above equation , ki is the axis rotation of the element at the i end and is calculated from Equation (15A.1) . The value of ki is obtained by subtracting Δ / l c from the value obtained by dividing the translation between the element nodes by the element net span, and the rotation value of the node i . In this way , the value of θ ki is obtained with the values obtained as a result of the linear calculation.
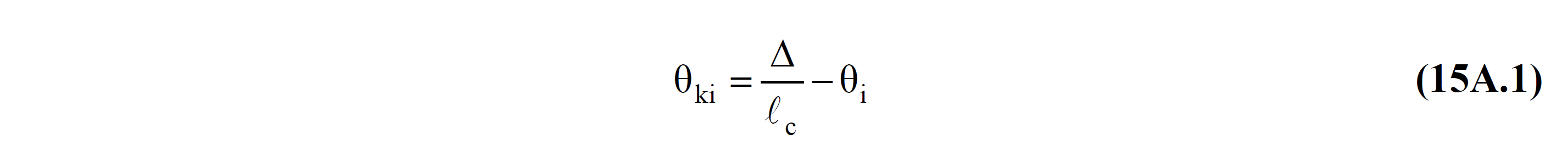
The θ yi value given in Equation (15A.2) is the yield rotation for frame elements and is calculated from Equation (15A.3) . In these equations, M yi and M yj are the effective yield moments at the ends i and j, respectively, and are calculated by the moment-curvature relationship derived from the section material model and the reinforcement layout. EI is the flexural stiffness of the unbroken section and is calculated from the section geometry.
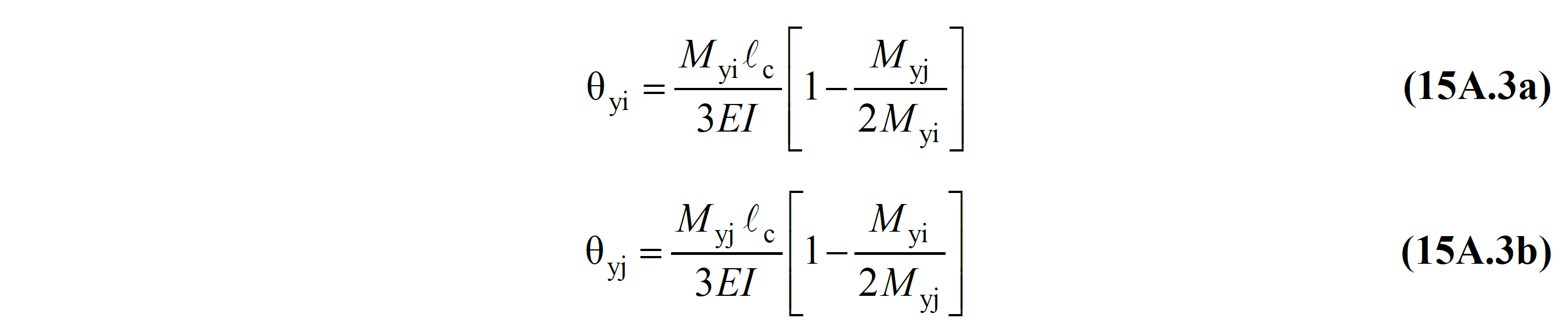
As can be seen above, as a result of the analysis made by linear earthquake calculation, the value of θ ki , the result of the moment curvature analysis calculated according to the section geometry and the reinforcement condition, the yi value is found. In this case, the plastic rotation demand θ pi value is found with the following equation according to Equation (15A.2) .
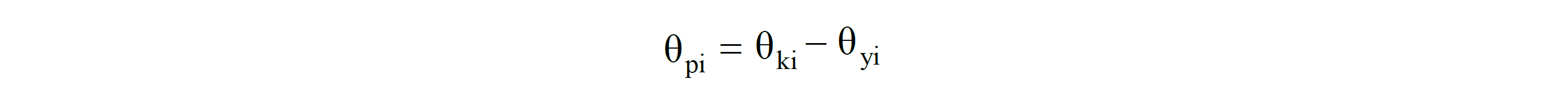
Evaluation and Design According to Strain of existing buildings as seen (ŞGDT) in determining the approach to seismic performance and linear calculation method used plastic rotation demand θ p , the value is calculated by the approximate expression obtained in a linear method. In this case, when the nonlinear seismic analysis methods applied plastic made by plastic hinge rotation θ p θ obtained by the linear method with p value to show affinity to a specific order but it will be the same.
