Composite Castellated Beam Design per AISC 360-16

How does ideCAD design composite castellated beams with steel-headed studs according to AISC 360-16?

Composite castellated beams with steel-headed stud design are made automatically per AISC 360-16.

The user can change composite slab design settings and secondary steel beam settings.

The flexural design of steel composite castellated beams according to AISC 360-16 is explained in detail under this title. Composite castellated beam design is done in two steps: Construction stage design and composite design.

Symbols

C_b : The lateral-torsional buckling modification factor
Z_x = Plastic section modulus about the x-axis, in.³ (mm³)
E: Modulus of elasticity of steel = 29,000 ksi (200 000 MPa)
F_y : Specified minimum yield stress of the type of steel being used, ksi
F_cr : Critical stress
K : Effective length factor
L: Laterally unbraced length of the member
P_r: Required axial force resistance for LRFD or ASD load combinations
P_c: Strength of axial compressive force available according to Section E
M_r: Required bending moment strength for LRFD or ASD load combinations
M_c: current bending moment strength according to Section F
r: Radius of gyration
λ: Width-to-thickness ratio for the element as defined in Section B4.1
λ_r : Limiting width-to-thickness ratio as defined in Table B4.1a
L_b : Length between points that are either braced against lateral displacement of the compression flange or braced against twist of the cross-section, in. (mm)
L_p : The limiting laterally unbraced length for the limit state of yielding, in. (mm)
L_r : The limiting unbraced length for the limit state of inelastic lateral-torsional buckling, in. (mm),
M_n : The nominal flexural strength
M_p : Plastic bending moment
S_x : Elastic section modulus taken about the x-axis, in.³ (mm³)

Composite castellated beam design is done in two steps: Construction stage design and composite design. The following conditions are checked in each design step.

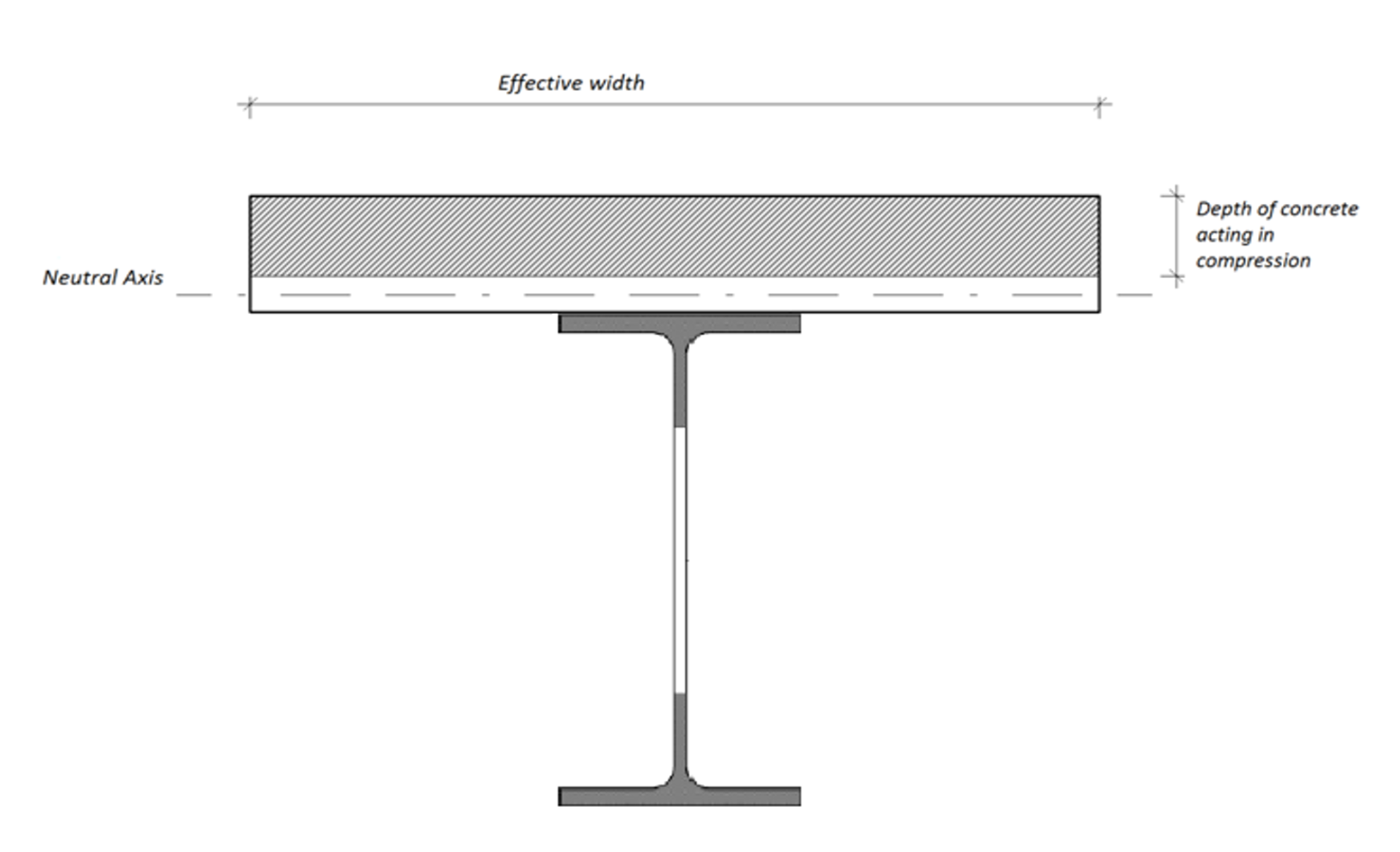
Construction Stage Design

Construction stage design is done with the lowest design ratio value obtained according to the limit states given below.

Biaxial Bending
Gross and Net Area Shear Check
Horizontal Shear Check
Web Post Buckling Check
Vierendeel Bending Check

The construction stage design cross-section sample is given below.

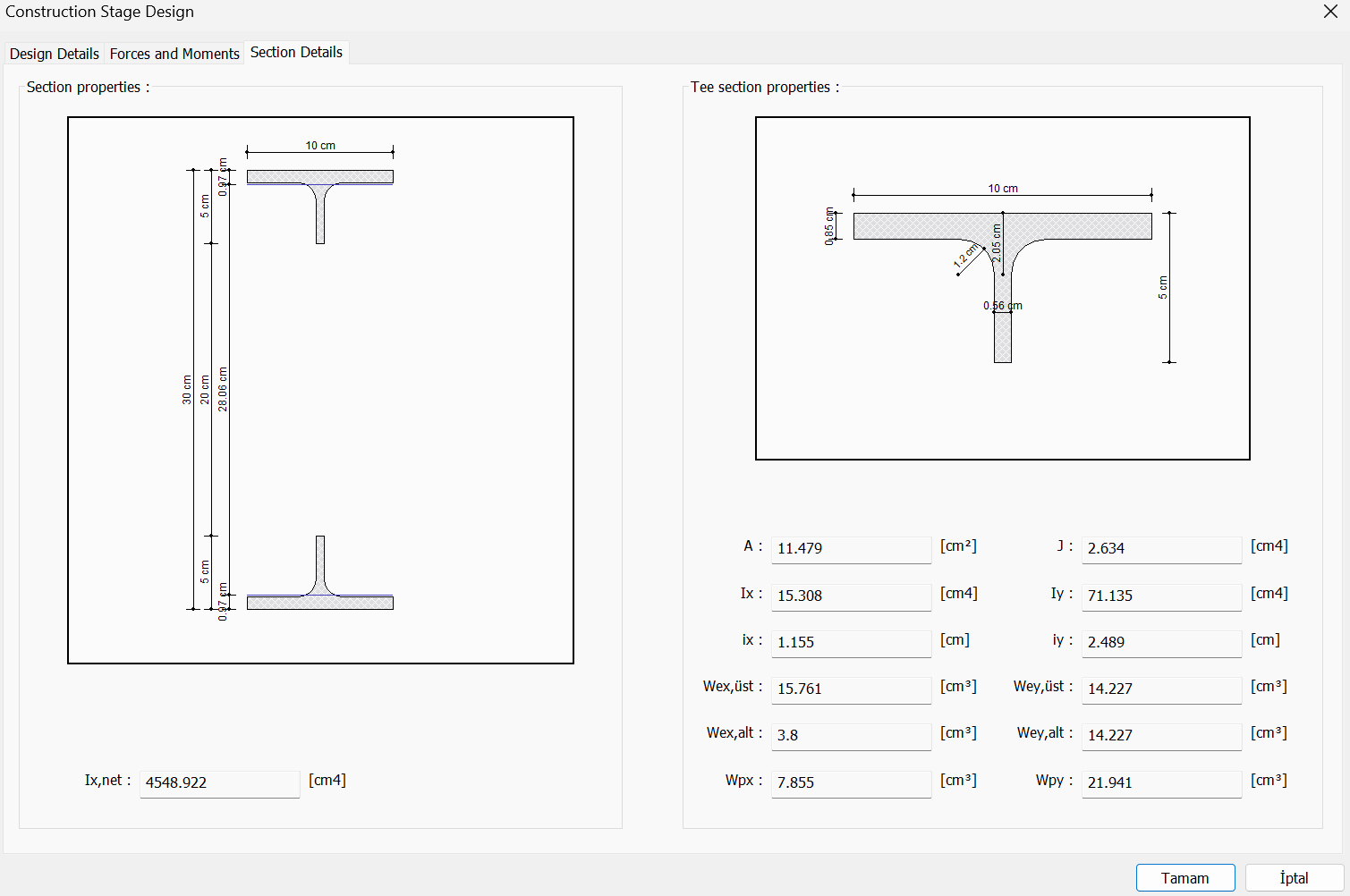
Composite Design

Composite castellated design is done with the lowest design ratio value obtained according to the limit states given below.

Gross and Net Area Shear Check
Horizontal Shear Check
Web Post Buckling Check
Vierendeel Bending Check
Deflection Check

The composite design cross-section sample is given below.

Biaxial Bending and Axial Force

Yielding Limit State

For the yield limit state, the nominal flexural strength, M_n, is calculated using the equation below by AISC 360-16.

When L_b ≤ L_p

When L_p < L_b ≤ L_r

When L_b > L_r

Axial Force

The axial compression capacity for the web part of the castellated beam is calculated as follows.

The critical stress, F_cr, is calculated as shown below.

When

When

Combined Forces

Equation H1.1 is used for biaxial and single symmetry axis members under combined axial compression and flexural moment.

Shear Control

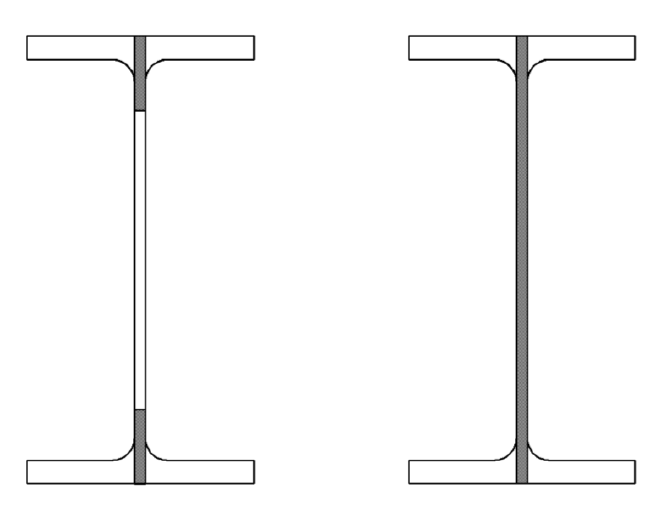
Gross and Net Area Shear Control

Shear control with the gross area is the whole web part of the castellated beam, while the shear control with the net area is calculated by considering the castellated beam's hollow section.

Horizontal Shear Control

The shear force on the castellated beam web is calculated using the balance equation and compared with the shear strength.

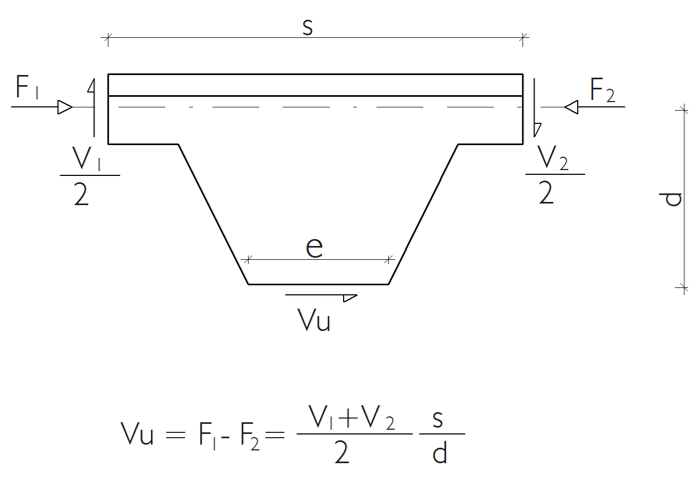
Vierendeel Bending Control

Axial Force and Biaxial Bending

The effects of the T section on the castellated beam spaces are found with the equilibrium equation. Internal force diagrams are used in the static analysis while calculating these forces. The equation of equilibrium calculates the bending moment and axial force on the T section. Then, the combined effects are considered by calculating the T-section bending and axial force strengths.

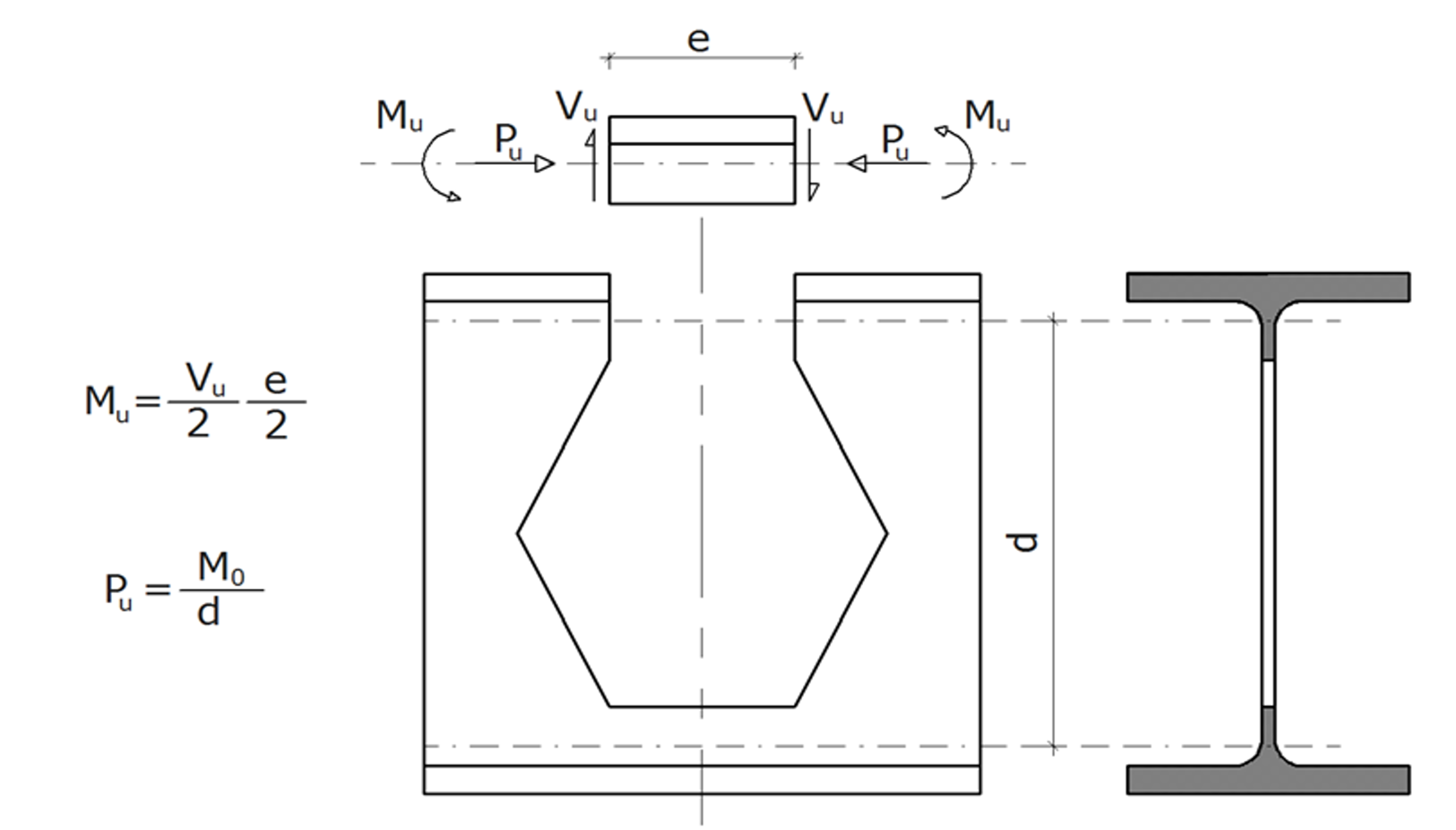
Web Post Buckling Control

Forces Acting on the Web

The bending moment values at the upper and lower boundaries of the web section between the castellated beam spaces are found, and lateral-torsional buckling is checked according to the rectangular section.

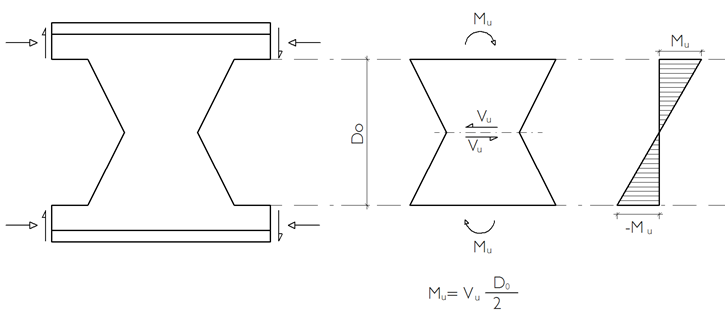
Web Post Buckling Strength

The web section between the castellated beam is calculated according to AISC 360-16 Section F.

The limit state of flange local buckling does not apply to sections with compact flanges.

The nominal flexural strength, M_n, is calculated below for sections with noncompact flanges.

The nominal flexural strength, M_n, is calculated below for sections with slender flanges.

Next Topic

Crane Beam Design per AISC 360-16

Related Topics