15A.3
Yield rotation value is calculated according to TBDY 15A.3 by using moment-curvature relation for column and beam elements for linear performance analysis . Moment-curvature analysis is done by considering the information level coefficient and the existing material strengths.
Yield rotation in frame elements (column and beam) is calculated automatically according to Equation (15A.3) .
Yield moments are calculated automatically using the moment-curvature relationship.
ICONS
E = Concrete modulus of elasticity
I = Moment of inertia
L p = Plastic hinge length
l c = Element net opening
M y = Effective yield moment
M yi = Effective yield momentat end i
M yj = Effective yield moment at end j
Δ = Element nodes translation
ϕ y = Yield curvature
ϕ t = Total curvature
θ p = Plastic rotation demand
θ y = Flow rotation
θ yi = flow rotation at end i
θ yj = flow rotation at end j
θ k = Displaced axis rotation
θ ki = displaced axis rotation at end i
Evaluation and Design According to Strain existing buildings (ŞGDT) in determining the approach to seismic performance and linear calculation method used element plastic rotation demand θ p or elements curvature lead the end section φ t is calculated in line method.
Linear performance analysis is performed with the principle of "the total deformation value in an element is equal to the sum of the elastic deformations and the plastic deformations in that element". Plastic deformations for ductile reinforced concrete elements are rotational deformations due to the moment effect. According to this approach, in order to find the plastic deformation value of an element, the total deformation value of that element is found and then the elastic deformations are subtracted from this value.
I edge of an element of plastic rotation demand θ p is calculated from the following equation.

Similarly, the total curvature demand ϕ t of an element is calculated from the following equation.
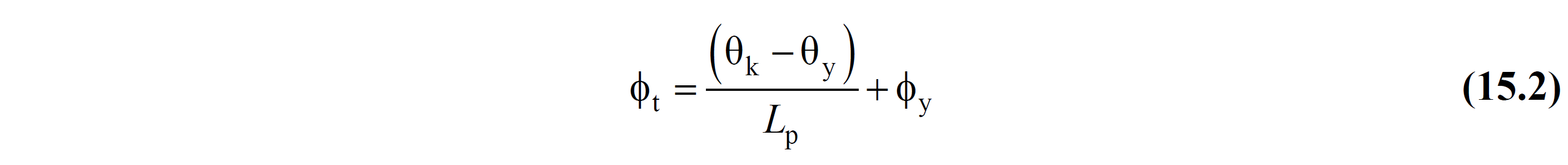
In these relations, θ yi refers to the return to flow at the node i. The flow return of an element at the ends of i and j is found by Equation (15A.3) for θ yi and θ yj .
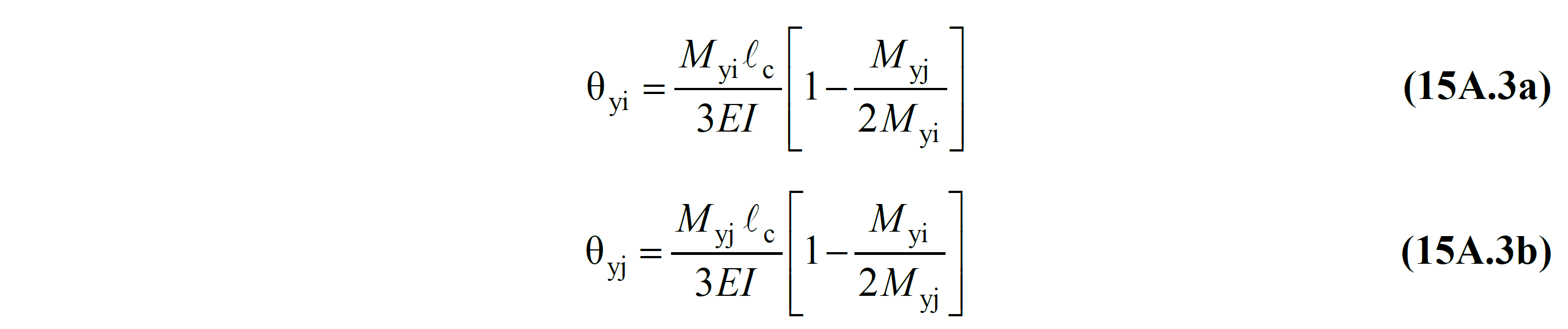
In these equations, M yi and M yj are the effective yield moments at the i and j ends , respectively. It is calculated by the moment-curvature relation calculated according to the material models and reinforcement placement, which are created by taking into account the existing material strengths with the coefficient of knowledge level M yi and M yj . The directions of the yield moments are counterclockwise plus and minus clockwise with respect to the local axes of the rod members . In this case, Equation (15A.3) includes both single curvature bending and double curvature bending because it is taken into account with signs . For unsymmetrical sections, the concept of direction affects the yield rotation values.
Axial force and biaxial bending interaction are taken into account while finding the M yi and M yj values of the columns .
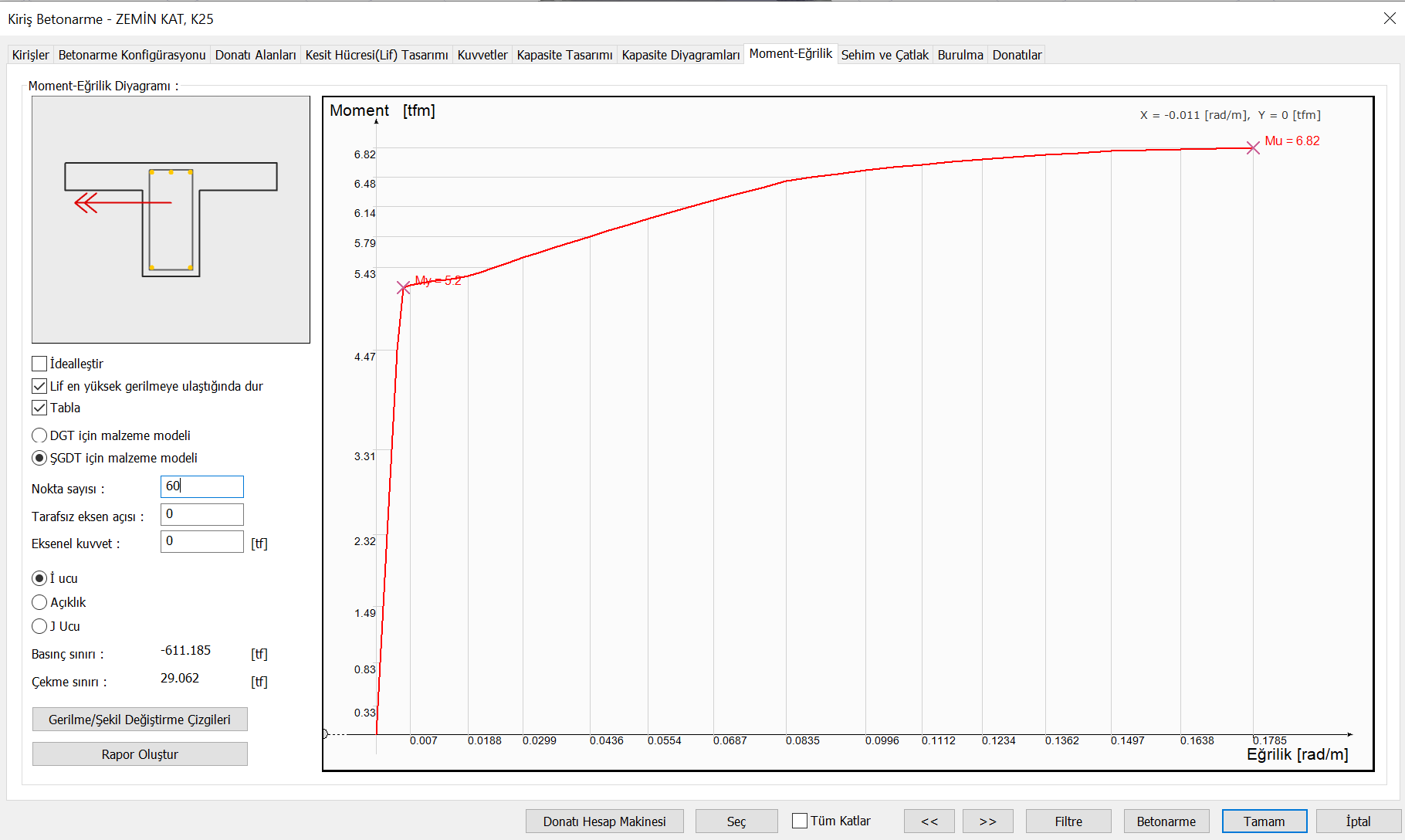
The moment curvature analysis of a beam element in the positive direction is shown below. In this case, the yield moment M y is the moment that occurs when the reinforcement at the bottom of the section flows.
Similarly, the following picture is shown for the moment curvature analysis in the negative direction. In this case, the yield moment M y is the moment that occurs when the reinforcement at the upper part of the section flows.
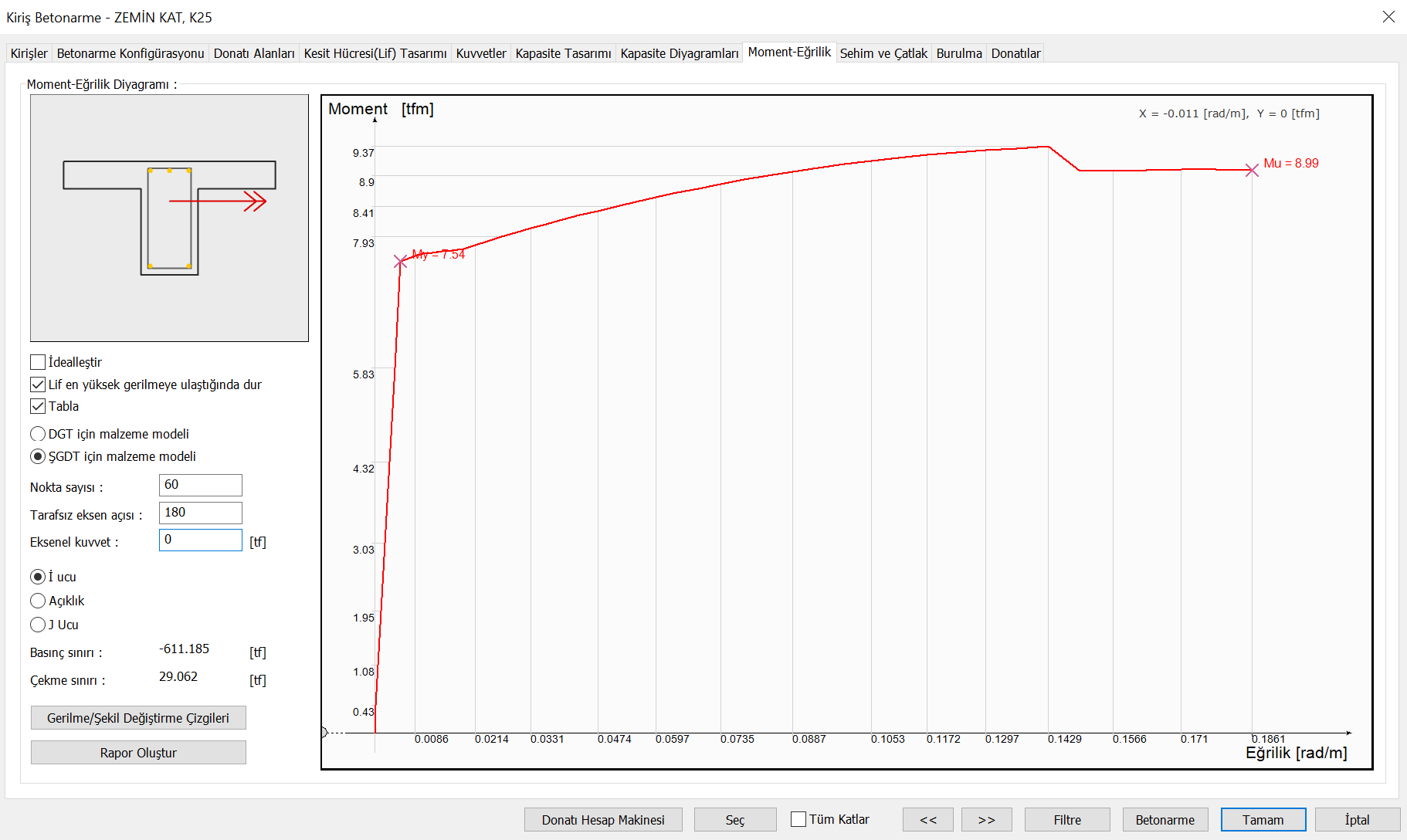
In Eq. (15A.3) , l c represents the clear opening. EI is the bending stiffness of the unbroken section. In this case, it is obtained by multiplying the elasticity module E of the concrete with the moment of inertia I of the section in the relevant direction.
As can be seen, if the linear calculation method is used to determine the earthquake performance of existing buildings with the Assessment and Design Based on the Shape Change (ŞGDT) approach, the yield rotation is not calculated with the relation θ y = ϕ y L p as in nonlinear calculations. Instead, it is calculated with the relations calculated with Equation (15A.3) .
Next Topic
