Axial strength or Combined Flexural and Axial Strength.
Nominal flexural and axial strength is calculated automatically.
Nominal axial compressive strength is calculated automatically.
Nominal axial tensile strength is calculated automatically.
İnternational Design Codes
ACI 318-19 : Axial strength or Combined Flexural and Axial Strength per ACI 318-19 with ideCAD
TSC 2018 : TSC Axial strength or Combined Flexural and Axial Strength
Notation in ACI
Ag = gross area of concrete section, in2
As = area of nonprestressed longitudinal tension reinforcement, in2
Ast = total area of nonprestressed longitudinal reinforcement, in2
α = depth of equivalent rectangular stress block, in.
bw = width of compression face of member, in.
c = distance from extreme compression fiber to neutral axis, in.
Cc = concrete compressive force, lb
Cs = reinforcement tension force, lb
fc' = specified compressive strength of concrete, psi
fy = specified yield strength for nonprestressed reinforcement, psi
Mn = nominal flexural strength at section, in.-lb
Pn = nominal axial compressive strength of member, lb
Pn,max = maximum nominal axial compressive strength of a member, lb
Pnt = nominal axial tensile strength of member, lb
Pnt,max = maximum nominal axial tensile strength of member, lb
Po = nominal axial strength at zero eccentricity, lb
ϕ = strength reduction factor
εt = net tensile strain in extreme layer of longitudinal tension reinforcement at nominal strength, excluding strains due to effective prestress, creep, shrinkage, and temperature
β1 = factor relating depth of equivalent rectangular compressive stress block to depth of neutral axis
Flexural Strength
Nominal flexural strength Mn and axial strength are calculated based on the following Design Assumptions.
Design assumptions
The flexural and axial strength of a member calculated by the strength design method, two basic conditions should be satisfied:
equilibrium
compatibility of strains
Equilibrium means balancing of forces acting on the element cross section at nominal strength. Stress-strain relationship for the concrete and the reinforcement at nominal strength is established within the design assumptions described follow:
Equilibrium is satisfied at each section.
It is assumed that strain in concrete and reinforcement is proportional to the distance from neutral axis.
Design strength is calculated by using these assumptions together with design assumptions for concrete described follow:
Maximum strain at the extreme concrete compression fiber is assumed equal to 0.003.
Tensile strength of concrete is neglected.
The relationship between concrete compressive stress and strain is represented by equivalent rectangular concrete stress distribution method.
Concrete stress of 0.85fc' is assumed uniformly distributed over. Equivalent rectangular concrete stress zone bounded by edges of the cross section and a line parallel to the neutral axis located a distance α from the fiber of maximum compressive strain, as calculated by:
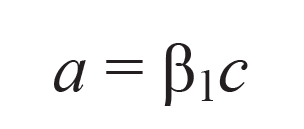
The distance between the fiber of maximum compressive stress and the neutral axis, c, is perpendicular to the neutral axis.
The value of β1 is determined using Codes.
Next Topic
