Basic Combinations with Seismic Load Effects
ICONS
E d (H) = Horizontal earthquake effect based on the design with directional coupling
E d (X) = earthquake effect in the direction of (X)
E d (Y) = earthquake effect in the direction of (Y)
E d (Z) = Vertical earthquake effect
G = Constant load effect
n = Live load participation coefficient
Q = Live load effect
Qe = Effectiveliveload effect
S = Snow load effect
TBDY Section 5.2.2. Combining Earthquake Impact with Other Effects
5.2.2.1 - The combination of the earthquake effect with the vertical load effect is defined in Equation (5.1) to be taken as a basis in the assessment of the structural system elements :
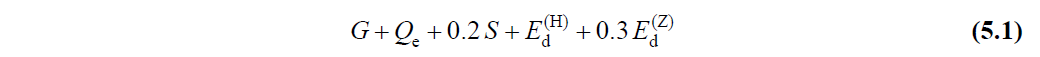
Where G is a constant load impact, snow load effect S, M d (Z) is 4.4.3 shows' e which is determined by the vertical seismic effects. The effective live load effect will be calculated as Q e = n Q using the Live Load Mass Participation Coefficient n defined in Table 4.3 . Horizontal seismic effect is defined in E d (H) 5.2.2.3 .
5.2.2.2 - Before the earthquake calculation to be made with the nonlinear calculation methods given in this section, a nonlinear static calculation shall be made in Equation (5.1 ) where the static vertical loads other than E d (H) are applied incrementally to the carrier system . Internal forces and deformations obtained from this calculation will be taken into account as initial values in the horizontal earthquake calculation. Nonlinear changes are not allowed at this stage in newly built and strengthened buildings. However, nonlinear deformations (if any) will also be taken into account as initial values in the assessment of existing buildings.
5.2.2.3 - E d (H) in Eq. (5.1) is defined as in (a) and (b) below :
(a) If the nonlinear horizontal earthquake calculation is made with the Repulsion Methods given in 5.6 , E d (H) , (X) and (Y) against the horizontal earthquake effect obtained by combining the separately calculated effects according to 4.4.2.1 . is coming.
(b) If the nonlinear horizontal earthquake calculation is made in the time domain according to 5.7 , the combined horizontal earthquake effect E d (H) , since the earthquake components in the horizontal (X) and (Y) directions are defined simultaneously according to 2.5 . is obtained directly as a result of this calculation.
Related Topics
