15.7.1.3
Unit deformation and plastic rotation limits (capacities) are calculated automatically in linear and nonlinear performance analysis of existing structures.
ICONS
d b = Diameter of longitudinal reinforcement (average in tension) [m]
L p = Plastic hinge length [m]
L s = Shear clearance [m]
ϕ y = Yield curvature [m -1 ]
ϕ u = Bending curvature [m -1 ]
ω we = ratio of mechanical reinforcement of effective confinement reinforcement
ε c (GÖ) = allowable confined concrete unit shortening limit for the Preventing collapse performance level
ε c (KH) = Controlled Damage allowed confined concrete unit shortening limit for performance level
ε c (SH) = allowed confined concrete unit shortening limit for Limited Damage performance level
ε c = unit strain value of concrete
ε s (GÖ) = allowable reinforcement steel for Pre- migration performance level the limit unit strain
ε s (CH) = Controlled Damage performance level the permissible limit of the deformation reinforcing steel unit
ε s (SH) = limited damage allowable reinforcement steel strain limit for performance level
ε su = reinforcement strain corresponding to maximum strength
θ p (KH) = allowable plastic rotation limit for Controlled Damage performance level [rad]
θ p (GÖ) = for Pre- Sink performance level Permissible plastic rotation limit [rad]
θ p (SH) = Allowable plastic rotation limit for Limited Damage performance level [rad]
Allowable unit deformation and plastic rotation limits when using linear calculation method or nonlinear calculation method in determining the earthquake performance of existing buildings with the Assessment and Design Based on Shaping (ŞGDT) approach TBDY Articles 5.8.1.1, 5.8.1.2, 5.8.1.3 and 5.8.1.4 ' are available as described.
Three performance levels (damage limits) are defined for ductile members cross sections. These are the Prevention of Migration (LO) Performance Level, Controlled Damage (KH) Performance Level, and Limited Damage (SA) Performance Level . In the performance analysis of existing buildings, the unit deformation and plastic rotation limits in each section for linear or nonlinear calculation methods are calculated according to these performance levels. The performance of the structure is determined by comparing the unit deformation and plastic rotation demands with the limit values mentioned above.
Plastic Deformation and Internal Force Limits for New Buildings

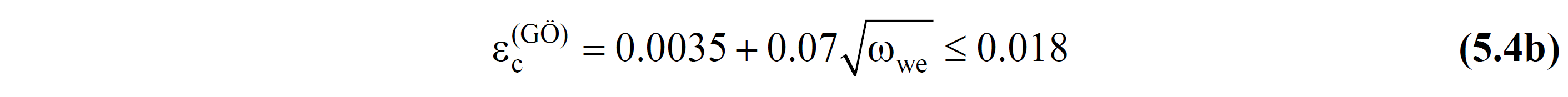
For the Prevention of Migration (LO) Performance Level , the unit deformation limit value of reinforcement steel ε s (GÖ) is given in Equation (5.5) . ε shows the unit elongation corresponding to the water reinforcement tensile strength. ε It is calculated according to ANNEX 5A , taking into account the Water Information Level Coefficient and Available Material Strengths .
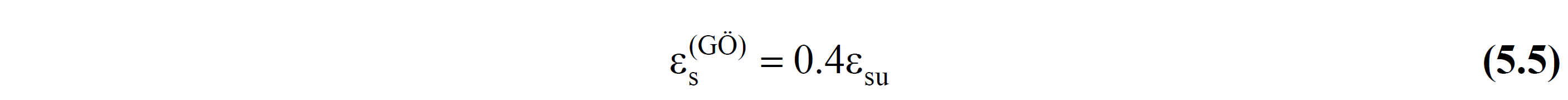
TBDY Article 5.8.1.2 according Preventing migrant (GO) Performance Level to be made for the performance evaluation of stacked plastic behavior model 'According limit for plastic rotations calculated value θ p (GO) , Eq. (5.6) is calculated by. In this relation, ϕ u represents the pre-crash curvature and ϕ y represents the yield curvature. The section in the plastic hinge of φ U and φ y values Knowledge Factor and Current Material Strengths taking into account Appendix 5 Collapse Prevention Performance Level for Concentrated Plasticity Model
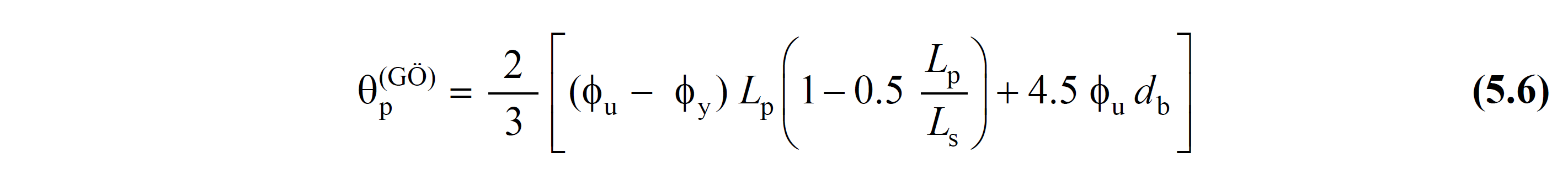
For the Controlled Damage (KH) Performance Level according to TBDY Article 5.8.1.3 , the unit deformation limit value ε c (KH) of the concrete material and the unit deformation limit value don s (KH) of the reinforcement steel is calculated by Equation (5.7a) . For the same performance level, the limit value θ p (KH) of plastic rotations calculated according to the Piled plastic behavior model is calculated by Equation (5.7b) .

According to Article 5.8.1.4 of TBDY , concrete material deformation limit value ε c (SH) and reinforcement steel strain limit value s (SH) for Limited Damage (SH) Performance Level are shown by Equation (5.8a) .
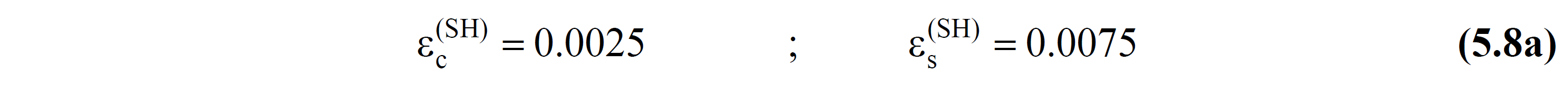
Damage Limited (SH) Performance Level to be made for performance evaluation in stacked plastic behavior model 'based on what limits for plastic rotation calculated value θ p (SH) , Eq. (5.8b) is calculated by. Where θ p (SH) plastic rotation is zero, it means there is no plasticization at this performance level.

If the linear calculation method is used to determine the earthquake performance of existing buildings with the Assessment and Design Based on Shaping (ŞGDT) approach, the above limit values are ε c (D) , ε c (KH) , ε c (SH) values for concrete and ε s ( for reinforcement steel ) . GÖ) , ε s (KH) , ε s (SH) limit values are used. Element performance at section level is determined by using unit deformation demands of concrete and reinforcement steel obtained by using element end curvature demand t ' found according to 15.7.1.1 .
In determining the earthquake performance of existing buildings with the Assessment and Design Based on Shaping (ŞGDT) approach, if an earthquake calculation is made with the nonlinear calculation method, the stacked plastic behavior model is used. In this case, the plastic rotation demand resulting from the thrust analysis is compared with the limit values θ p (GÖ) , θ p (KH) and θ p (SH) and the element performance at the section level is determined.

Next Topic
Related Topics
