Column Combined Flexural and Axial Design per ACI 318-19 with ideCAD

How does ideCAD calculate columns' combined flexural and axial strength according to ACI 318-19?

• The three-dimensional interaction failure surface of a column is calculated automatically.

• Demand/Capacity Ratio of Columns is calculated automatically.

Notation

A_g = gross area of concrete section, in²
A_s = area of nonprestressed longitudinal tension reinforcement, in²
A_st = total area of nonprestressed longitudinal reinforcement, in²
α = depth of equivalent rectangular stress block, in.
b_w = width of compression face of member, in.
c = distance from extreme compression fiber to neutral axis, in.
C_c = concrete compressive force, lb
C_s = reinforcement tension force, lb
d = distance from extreme compression fiber to centroid of longitudinal tension reinforcement, in.
D = dead load
E = earthquake load
f_c^' = specified compressive strength of concrete, psi
f_y = specified yield strength for nonprestressed reinforcement, psi
L = live load
L_r = roof live load
M_n = nominal flexural strength at section, in.-lb
M_u = factored moment at section, in.-lb
P_n = nominal axial compressive strength of member, lb
P_n,max = maximum nominal axial compressive strength of a member, lb
P_nt = nominal axial tensile strength of member, lb
P_nt,max = maximum nominal axial tensile strength of member, lb
P_o = nominal axial strength at zero eccentricity, lb
P_u = factored axial force; to be taken as positive for compression and negative for tension, lb
R = rain load
S = snow load
T_n = nominal torsional moment strength, in.-lb
T_u = factored torsional moment at section, in.-lb
V_n = nominal shear strength, lb
V_u = factored shear force at section, lb
W = wind load
ϕ = strength reduction factor
ε_t = net tensile strain in extreme layer of longitudinal tension reinforcement at nominal strength, excluding strains due to effective prestress, creep, shrinkage, and temperature
β₁ = factor relating depth of equivalent rectangular compressive stress block to depth of neutral axis

Required strength

The required strength is calculated in accordance with the factored load combinations in Load Factors and Combinations per ACI 318-19 with ideCAD title. Combined Axial and Flexural Required strengths of a column P_u and M_u occur simultaneously for a column. Therefore, for each applicable factor load combination specified in ACI Table 5.3.1, the most unfavorable condition of P_u and M_u occurring simultaneously is considered.

Design strength

Design strength in all sections should satisfy all conditions given below;

• ϕP_n ≥ P_u

• ϕM_n ≥ M_u

• ϕV_n ≥ V_u

• ϕT_n ≥ T_u

Strength reduction factors ϕ is determined according to using ACI Table 21.2.2.

P_n and M_n are calculated in accordance with Axial strength or Combined Flexural and Axial Strength per ACI 318-19 with ideCAD title. Combined Axial and Flexural strengths create a three-dimensional interaction failure surface. In addition to axial compression and biaxial bending, the formulation allows for axial tension and biaxial bending considerations. An interaction surface of a column is shown below.

P_n means nominal axial compressive strength, and M_n means nominal flexural strength. M_n takes different values for each axial force level. Therefore, a three-dimensional interaction failure surface is formed in the picture above. Nominal flexural strength M_n is calculated according to the assumptions described in Flexural Strength per ACI 318-19 with ideCAD title. Flexural design strength ϕM_n is obtained by calculating M_n and strength reduction factor ϕ at each axial force level. While finding the flexural design strength, combined with axial force ϕM_n, it should be found in which control zone the cross-section is. When the section is tension controlled, a ϕ factor for tension control is used. The ϕ factor for compression is used when the section is compression controlled.

As described in the title of Axial strength or Combined Flexural and Axial Strength per ACI 318-19 with ideCAD, for nonprestressed concrete members nominal axial strength P_o and the maximum design compressive strength ϕP_n,max values are calculated as given below;

Nominal flexural strength M_n with zero compression is calculated as described in the title of Flexural Strength per ACI 318-19 with ideCAD. Similarly, with the same design assumptions, combined nominal flexural and axial strength M_n and P_n are calculated as shown below.

From the equation of equilibrium:

Nominal flexural strength M_n:

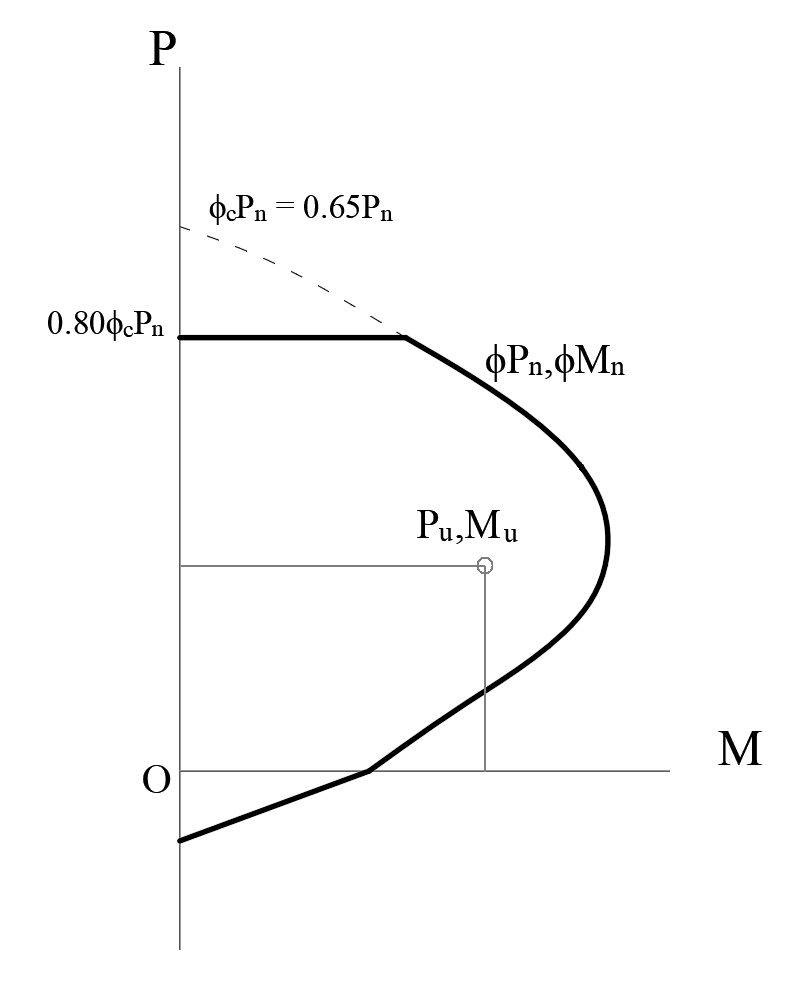
Demand/Capacity Ratio of Columns

Because of the axial force and biaxial bending interaction in the columns, the demand/capacity ratio is calculated using the interaction curve. The point (P_u,M_u) is placed in the interaction space shown as point D in the picture below. If point D (P_u,M_u) is within the acceptable range, the column capacity is adequate. However, if the point D (P_u,M_u) is outside the interaction volume, the column is overstressed. The capacity ratio is calculated using point C obtained by extending the line passing through points O and D to the interaction curve. The capacity ratio is given by the ratio OD/OC.

Next Topic

Column Shear Design per ACI 318-19 with ideCAD

Related Topics

• Minimum Flexural Strength of Columns per ACI 318-19 with ideCAD

• Reinforced Concrete Column Design Limits per ACI 318-19 with ideCAD

• Column Reinforcement Limits per ACI 318-19 with ideCAD

• Column Reinforcement Detailing per ACI 318-19 with ideCAD

• Application of Load Combinations to Modal Response Spectrum Analysis