Application of Complete Quadratic Combination (CQC) Rule
In each push step, dynamic responses are determined for all modes and the structural equivalents are determined automatically by the TKB (CQC) method.
In the i'th step of the thrust analysis with the ARSA method, the structural responses calculated separately for the (X) and (Y) earthquake directions, i.e. typical displacement, plastic deformation or internal force values r x (i) and r y (i ) is expressed with.

Full Quadratic Combination (TKB or CQC) rule is explained in Annex 4B.2.4 of TBDY Section . Accordingly, (X) and (Y) for the earthquake direction, at the end of the i th thrust step, any displacement, plastic deformation or internal forces occurring at any point or section of the carrier system and It is calculated with the following equations.
:r_cizgi_yi::r_cizgi_xi:

In this equation, m and n represent the number of modes, x and y represent the earthquake direction. for example (X) in the i'th step of the thrust analysis in the earthquake direction, belonging to a typical n'th natural vibration mode Determination of Internal Forces for Each Direction and Mode and using the above equations, in other words by combining the CQC method. and values are obtained.
:r_cizgi_yi::r_cizgi_xi::r_cizgi_yni::r_cizgi_xni::art_ölç_kat::r_cizgi_xni:
In the above equation, ρ shows the cross correlation coefficient of the mn , m and n modes . According to TBDY Equation 4B.5a , ρ mn is calculated by the following equation.
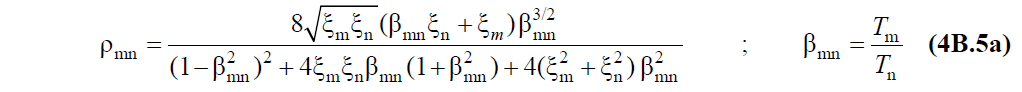
Wherein β mn , taken into account the ratio of the m-th and n-th natural vibration period, ξ m and ξ n are within the same mode and modal damping factors can be different from each other 's is shown.
When these processes are applied, typical displacement, plastic deformation or internal force values r x (i) and r y (i) are calculated for the earthquake direction (X) and (Y) at the end of step i .
