15A.4
Yield rotation value for shear walls is calculated according to TBDY 15A.4 using the moment-curvature relation for linear performance analysis . Moment-curvature analysis is done by considering the information level coefficient and the existing material strengths.
Yield rotation in curtain elements is calculated automatically according to Equation (15A.4) .
Yield moments are calculated automatically using the moment-curvature relationship.
ICONS
E = Concrete modulus of elasticity
I = Moment of inertia
L p = Plastic hinge length
l c = Element net opening
M y = Effective yield moment
ϕ y = Yield curvature
ϕ t = Total curvature
θ p = Demand for plastic rotation
θ y = Flow rotation
θ yi = flow rotation at end i
θ k = Displaced axis rotation
θ ki = displaced axis rotation at end i
Evaluation and Design According to Strain existing buildings (ŞGDT) in determining the approach to seismic performance and linear calculation method used element plastic rotation demand θ p or elements curvature lead the end section φ t is calculated in line method.
Linear performance analysis is performed with the principle of "the total deformation value in an element is equal to the sum of the elastic deformations and the plastic deformations in that element". Plastic deformations for ductile reinforced concrete elements are rotational deformations due to the moment effect. According to this approach, in order to find the plastic deformation value of an element, the total deformation value of that element is found and then the elastic deformations are subtracted from this value.
I edge of an element of plastic rotation demand θ p is calculated from the following equation.
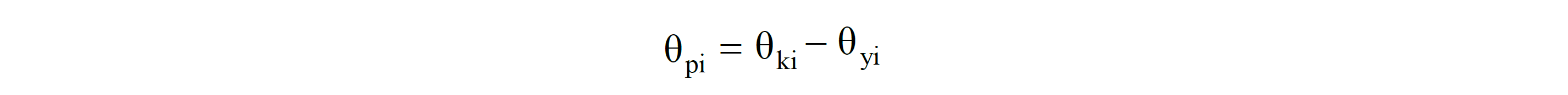
Similarly, the total curvature demand ϕ t of an element is calculated from the following equation.
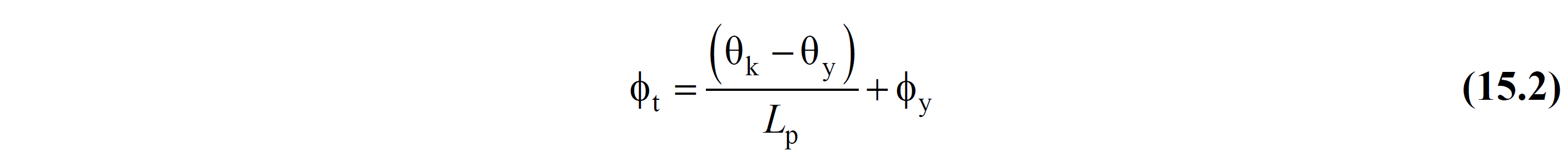
In these relations, θ yi refers to the return to flow at the node i. Return flow to the lower end of the shielding member θ y Eq. (15A.4) is calculated by.
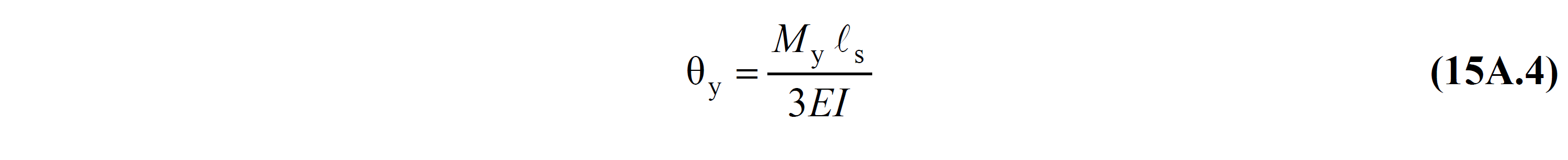
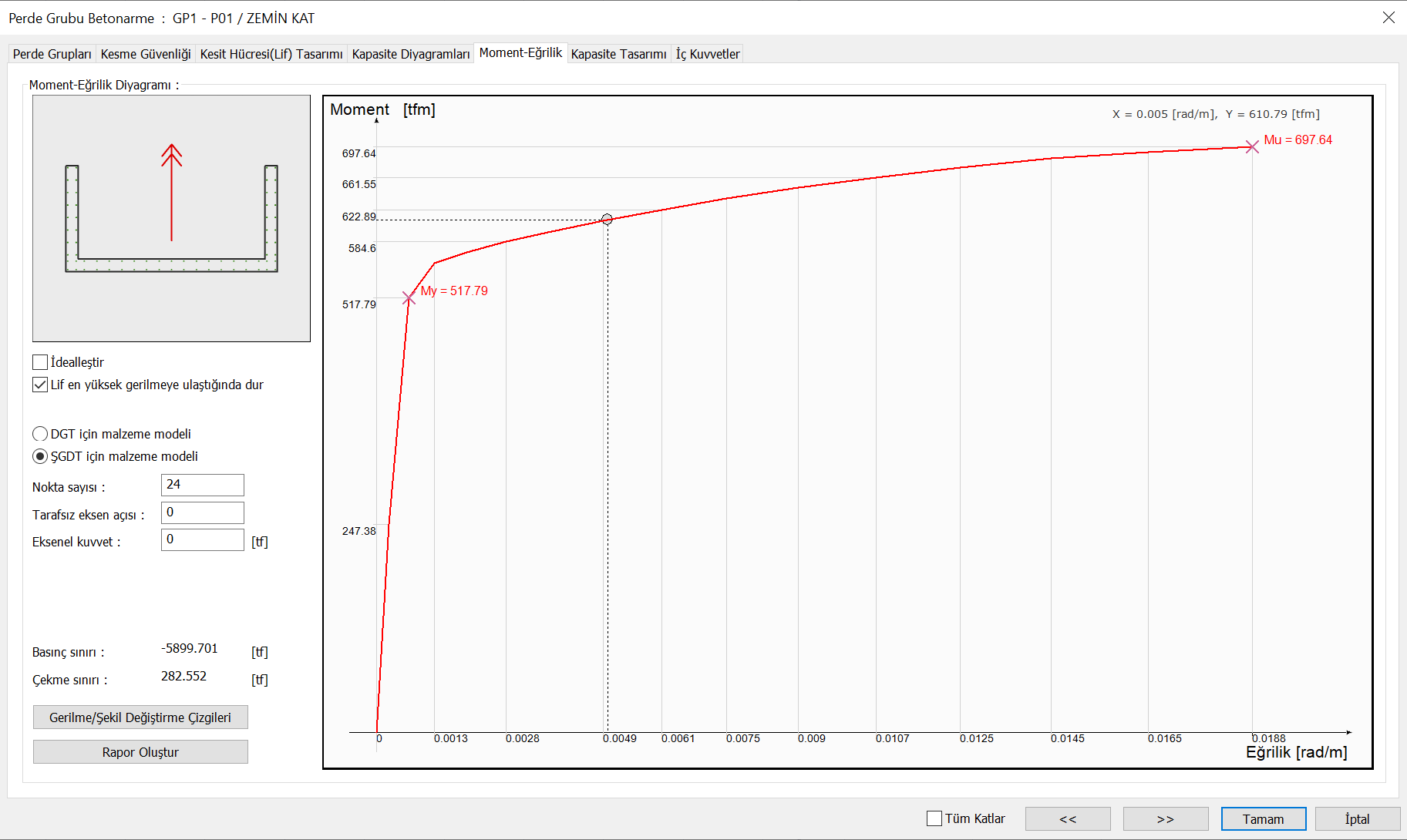
In these equations, M y is the effective yield moment of curtain . The M y value is calculated with the information level coefficient and the moment-curvature relationship calculated according to the material models and reinforcement placement, which are created considering the existing material strengths . In reinforced concrete walls with cross-section shape I, T, L, U or C, the resultant of the finite element joint forces are obtained as equivalent rod section effects at the cross-section gravity center, based on the reinforced concrete section calculation. Similarly, in reinforced concrete walls with cross-sectional shape I, T, L, U or C from the center of cross-section gravity, the effective yield moment M y is found as a result of the moment curvature analysis as shown below.
Next Topic
