Beam Shear Design per ACI 318-19 with ideCAD

How does ideCAD calculate beams' shear strength according to ACI 318-19?

Beam design shear strengths are calculated automatically.

Beam required shear strengths are calculated automatically.

Notation

A_v = area of shear reinforcement within spacing s, in.²
A_v,_min = minimum area of shear reinforcement within spacing s, in.²
b_w= width of compression face of member, in.
c₁= dimension of rectangular or equivalent rectangular column, capital, or bracket measured in the direction of the span for which moments are being determined, in.
d = distance from extreme compression fiber to centroid of longitudinal tension reinforcement, in.
D = dead load
E = earthquake load
f_c^'= specified compressive strength of concrete, psi
f_y= specified yield strength for nonprestressed reinforcement, psi
f_yt= specified yield strength of transverse reinforcement, psi
l_n = length of clear span measured face-to-face of supports, in.
l_u = unsupported length of column or wall, in.
L = live load
L_r = roof live load
M_n= nominal flexural strength at section, in.-lb
M_pr = probable flexural strength of members, with or without axial load, determined using the properties of the member at joint faces assuming a tensile stress in the longitudinal bars of at leasts 1.25f_y and a strength reduction factor ϕ of 1.0, in.-lb
P_n = nominal axial compressive strength of member, lb
P_u = factored axial force; to be taken as positive for compression and negative for tension, lb
R = rain load
S = snow load
s = center-to-center spacing of items, such as longitudinal reinforcement, transverse reinforcement, tendons, or anchors, in.
T_n = nominal torsional moment strength, in.-lb
T_u = factored torsional moment at section, in.-lb
V_c= nominal shear strength provided by concrete, lb
V_e= design shear force for load combinations including earthquake effects, lb
V_e^b= Capacity shear force of the column based on the maximum probable moment strengths of the beams framing into the column, lb
V_e^c= Capacity shear force of the column based on the maximum probable flexural strengths of the two ends of the column, lb
V_n= nominal shear strength, lb
V_s= nominal shear strength provided by shear reinforcement, lb
V_u= factored shear force at section, lb
V_u,z= factored load per unit length of beam or one-way slab, lb/in.
W = wind load
ϕ = strength reduction factor
Ω_o = overstrength factor for the lateral-force-resisting system given in ASCE Table 12.2-1.

Beam required strength is calculated in accordance with the factored load combinations in Load Factors and Combinations per ACI 318-19 with ideCAD title. The required shear strength of a beam V_u is obtained from Load Combinations given in ACI Table 5.3.1.

Shear design strength at all sections should satisfy the condition ϕV_n ≥ V_u.

Strength reduction factors ϕ is determined according to using ACI Table 21.2.1. Interaction between load effects is considered.

Nominal one-way shear strength at a column, V_n, is calculated by:

The nominal shear strength V_n is calculated as the sum of the nominal shear strength provided by concrete, V_c, and nominal shear strength provided by shear reinforcement V_s as shown in ACI Eq.(22.5.1.1).

The nominal shear strength V_n for a column is calculated in accordance with One-Way Shear Strength per ACI 318-19 with ideCAD title. In addition, V_s and V_c calculations are also described in the same title with details.

At each section of a beam where V_u > ϕV_c, transverse reinforcement is provided such that ACI Eq. (22.5.8.1) should be satisfied.

Vs is calculated using ACI Eq. (22.5.8.5.3) for a beam reinforced with transverse reinforcement.

A_v is the effective area of all bar legs or wires within spacing s, for each rectangular tie, stirrup, hoop, or crosstie. For each circular tie or spiral, A_v is two times the area of the bar or wire within spacing s.

Using equations ACI Eq. (22.5.8.1) and ACI Eq. (22.5.8.5.3), the required area of shear reinforcement, A_v,and its spacing, s can be calculated as follows.

According to ACI 9.6.3.4; If shear reinforcement is required, A_v,_min is equlat to the greater of the following relations;

A minimum area of shear reinforcement, A_v,_min should be provided in all sections where V_u > 0.5ϕV_c.

Strength reduction factors ϕ is determined according to using ACI Table 21.2.1.

Beams of Earthquake Resistant Structures must satisfy (A_v)_min condition.

Shear Design for Columns of Earthquake Resistant Structures

Ordinary moment frames

All the conditions and calculations described above are valid for beams of ordinary moment frames.

Intermediate moment frames

All the conditions and calculations described above are valid for beams of intermediate moment frames.

According to ACI 18.4.2.3; the Design shear strength of a beam, ϕV_n, should be less than both two conditions given below;

The sum of the shear force is determined from a free-body diagram obtained by cutting through the beam ends, with end moments assumed equal to the nominal moment strengths and the shear calculated for factored gravity and vertical earthquake loads.
The maximum shear force obtained from design load combinations include the earthquake effect E, which should be doubled. In other words, the overstrength factor, Ω_o, is considered as 2. For example, when calculating design shear force, the combination Eq.(5.3.1e) defined in ACI Table 5.3.1 should be considered as follows.

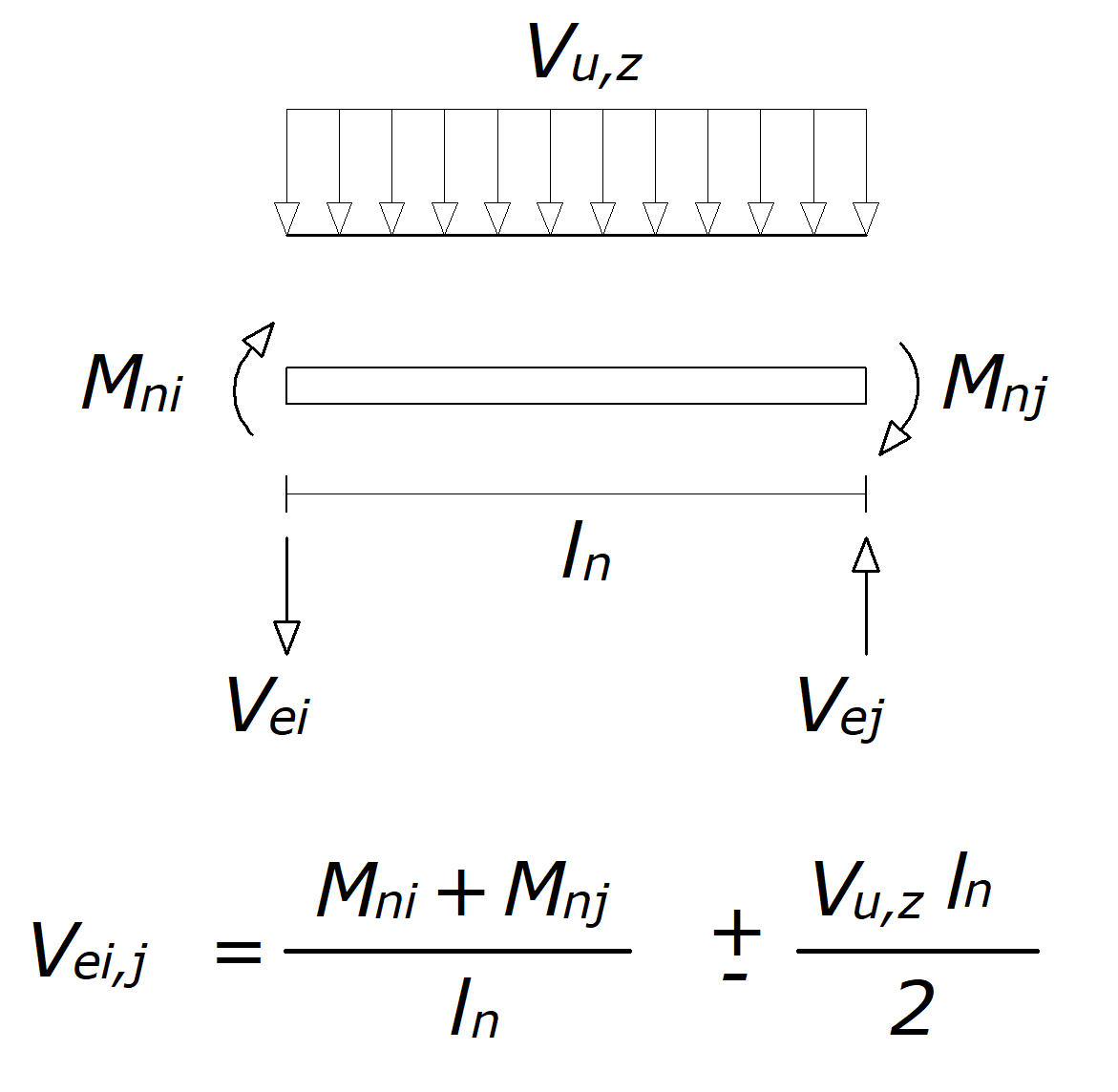
According to Condition 1, the factored shear force is determined from a free-body diagram obtained by cutting the beam ends. In addition, the moments at the beam ends are assumed to be nominal moment strengths acting in reverse curvature bending, both clockwise and counterclockwise. To determine the maximum beam shear, it is assumed that nominal moment strengths, M_n,(ϕ=1.0 for the moment) occur simultaneously at both ends of its clear span. ACI Figure R18.4.2 demonstrates only one of the two options that are to be considered for every beam. This process is applied in all load combinations.

Special moment frames

The design shear force V_e, is calculated by assuming that moment capacities, M_pr, occurs at each end of the beam. That moment of opposite sign corresponding to probable flexural strength, M_pr, acts at the joint faces. It is also assumed that the beam has factored in gravity and vertical earthquake loads along its span.

As shown in ACI Figure R18.6.5, the clockwise rotation of the joint at one end and the associated counter-clockwise rotation of the other joint produce one shear force. In other words, the shear force is determined from a free-body diagram obtained by cutting the beam ends, with end moments assumed equal to the nominal moment strengths. M_pr1 and M_pr2 are calculated by using a strength reduction factor, ϕ of 1.0, and longitudinal reinforcement with an effective yield stress equal to 1.25f_y.

According to ACI 18.6.5.2, if both two conditions given below occur, transverse reinforcement over the lengths l_o should be designed to resist shear, assuming V_c=0.

The earthquake-induced shear force, calculated in accordance with ACI 18.6.5.1, is at least one-half of the maximum required shear strength within l_o.
The factored axial compressive force P_u including earthquake effects, is less than A_gf_c′/20.

Next Topic

Beam Reinforcement Limits per ACI 318-19 with ideCAD

Related Topics