Deflection Control
Deflection control is done automatically.
ICONS
Ec = Modulus of elasticity of concrete
fctd = Design tensile strength of concrete
Icr = Cracked sectional moment of inertia relative to the neutral axis
Ief = Effective moment of inertia
Ic = Gross sectional moment of inertia
ln = Clear span of the member
Mcr = Cracking moment of member under bending
Mmax = Maximum bending moment for member
y = Distance between extreme tension fiber and neutral axis
δt = Total deflection
δi = Instantaneous deflection
δig = Instantaneous deflection due to permanent loads
γt = Time-dependent factor for permanent load
λ = Permanent deflection multiplier
ρ' = Ratio of compression reinforcement
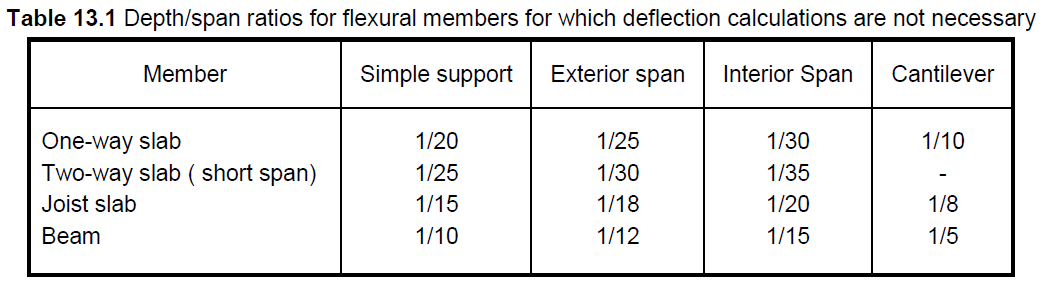
13.2 - DEFLECTION CONTROL
13.2.1 - General Regulations
In members subjected to flexures, such as slabs and beams, deflections that would impair their function,
affect their appearance, and cause cracking or crushing in adjacent non-structural connected members
should not be allowed to occur. Immediate deflections due to permanent and live loads and deflections due
to shrinkage and creep effects for these members should be computed by considering their cracked state.
In the case of beams and especially slabs, which do not support or are not attached to nonstructural
members sensitive to deflections and whose depth to span length ratios are within the limits given in Table
13.1, deflection calculations need not be carried out.
If more reliable methods based on the principles of structural mechanics, which also take reinforced concrete
behavior into account is not used, the immediate deflections can be calculated by using the approximate
the method given in Clause 13.2.2 and the time-dependent deflections by the method presented in Clause
13.2.3.
13.2.2 - Approximate Calculation for Instantaneous Deflection
Instantaneous deflection values of reinforced concrete flexural members under permanent and live loads
with uncracked sections in the span (Mmax ≤ Mcr) should be calculated in accordance with structural
mechanics principles by using the gross sectional moment of inertia.
For cracked sections (Mmax > Mcr), the instantaneous deflection should be calculated as given above using
the effective moment of inertia values obtained from Equation 13.1 and by considering support conditions.
The modulus of elasticity Ec to be used in this calculation should be taken from Section 3.3.

The cracking moment for the section should be calculated in accordance with Section 13.2. For continuous
beams and slabs, the two-moment of inertia values of the span section and the support section (average of
two supports) should be calculated separately by using Equation13.1 and then the average of these two
values should be used as the effective moment of inertia. In the case of cantilevers, the moment of inertia of
the support section should be used as the effective moment of inertia.
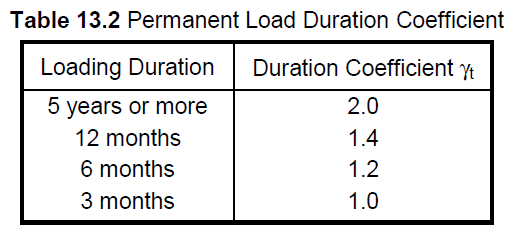
13.2.3 - Time-Dependent Deflection Calculation
Calculation of additional long-term deflections due to shrinkage and creep in reinforced concrete structures
should be made in accordance with Clause 3.3.4. If more precise calculations are not required, the total
deflection, including the time-dependent deflection can be obtained by using Equation 13.3.

The coefficient γt in the equation should be taken from Table 13.2 according to the effective time of the permanent loads. ρ' is the ratio of compression reinforcement in the section.
The coefficient, γt, in the above equation, which depends on the duration of the permanent loading, can be
obtained from Table 13.2. ρ' is the ratio of compression reinforcement in the section.
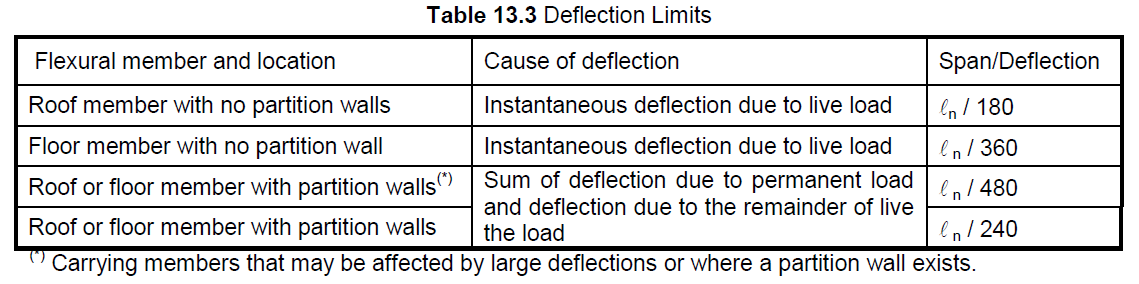
13.3 - Deflection Limits
Allowable maximum deflections for flexural members are given in Table 13.3: ln is the clear span.
Next Topic
