Effective Section Stiffness of Structural System Elements
ICONS
d b = Diameter of longitudinal reinforcement (average in tensile) [m]
(EI) e = Effective section stiffness of column, beam, tie beam or curtain modeled according to the agglomerated plastic behavior
f y = Average (expected) yield strength of reinforcing steel [MPa]
f ce = Average (expected) compressive strength of concrete [MPa]
h = Section height [m]
L s = Shear opening [m]
M y = Effective yield moment [kNm]
ϕ y = Curvature of yield [m -1 ]
θ y = Flow Status to the axis of rotation likelihood disposition [rad]
η = in the calculation of the first rotation Pour beams and columns, curtains received coefficient 0.5
TBDY Section 5.4.5. Effective Section Stiffness of Reinforced Concrete Bearing System Elements
5.4.5.1 - Effective cross-section stiffness multipliers regarding in-plane and out-of-plane behavior of linearly modeled walls and slabs shall be taken from Table 4.2 in 4.5.8 .
5.4.5.2 - Effective cross-section stiffness of columns, beams, tie beams and walls modeled according to the piled plastic behavior will be determined according to Equation (5.2) .

Here, M y and θ y show the average of the effective yield moments and yield rotation of the plastic hinges at the ends of the rod element . L s is the shear gap (ratio of moment / shear force in cross section); It can be taken as approximately half the span in columns and beams, and half the distance from the base of each floor to the top of the curtain for curtains. The rotation of plastic hinge flow θ y in Equation (5.2) shall be calculated by Equation (5.3) :
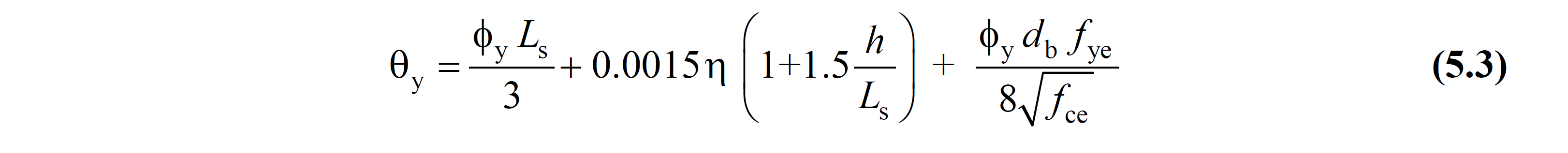
Here ϕ y indicates the effective curvature flow in the plastic joint cross section. It will be taken η = 1 for beams and columns and η = 0.5 for walls. h is the section height. Flow conditions for reinforcement stripping rotation expressing last term containing D b support (nodes or base A) Average diameter of the interlocking reinforcing steel, f ce and f to the concrete of the average (expected) shows the yield strength average of reinforcement compressive strength.
