TSC Flexural Strength

• Flexural strength is calculated automatically.

Notation

A_s = area of nonprestressed longitudinal tension reinforcement, mm²
a = depth of equivalent rectangular stress block, mm.
b_w = web width or diameter of circular section, mm.
c = distance from extreme compression fiber to neutral axis, mm.
C_c = concrete compressive force, kN
C_s = reinforcement tension force, kN
d = distance from extreme compression fiber to centroid of longitudinal tension reinforcement, mm.
f_ck = specified compressive strength of concrete, MPa
f_cd = design compressive strength of concrete, MPa
f_yk = specified yield strength for nonprestressed reinforcement, MPa
f_yd = design yield strength for nonprestressed reinforcement, MPa
M_d = desing flexural strength at section, kNm
M_n = nominal flexural strength at section, kNm
γ = strength reduction factor
ε_s = net tensile strain in extreme layer of longitudinal tension reinforcement at nominal strength, excluding strains due to effective prestress, creep, shrinkage, and temperature
k₁ = factor relating depth of equivalent rectangular compressive stress block to depth of neutral axis

Flexural Strength

Nominal flexural strength M_n is calculated based on the following Design Assumptions. Acconrding to TS500 Chapter 7, design strength of a section is defined as M_d.

Design assumptions

The flexural and axial strength of a member calculated by the strength design method, two basic conditions should be satisfied:

1. equilibrium

2. compatibility of strains

Equilibrium means balancing of forces acting on the element cross section at nominal strength. Stress-strain relationship for the concrete and the reinforcement at nominal strength is established within the design assumptions described follow:

• Equilibrium is satisfied at each section.

• It is assumed that strain in concrete and reinforcement is proportional to the distance from neutral axis.

Design strength is calculated by using these assumptions together with design assumptions for concrete described follow:

• Maximum strain at the extreme concrete compression fiber is assumed equal to 0.003.

• Tensile strength of concrete is neglected.

• The relationship between concrete compressive stress and strain is represented by equivalent rectangular concrete stress distribution method.

• Concrete stress of 0.85f_cd is assumed uniformly distributed over. Equivalent rectangular concrete stress zone bounded by edges of the cross section and a line parallel to the neutral axis located a distance a from the fiber of maximum compressive strain, as calculated by:

• The distance between the fiber of maximum compressive stress and the neutral axis, c, is perpendicular to the neutral axis.

• The value of k₁ is determined using TS500 Table 7.1.

The design strength of concrete and reinforcement materials is given below.

Desing flexural strength M_d is calculated as shown below.

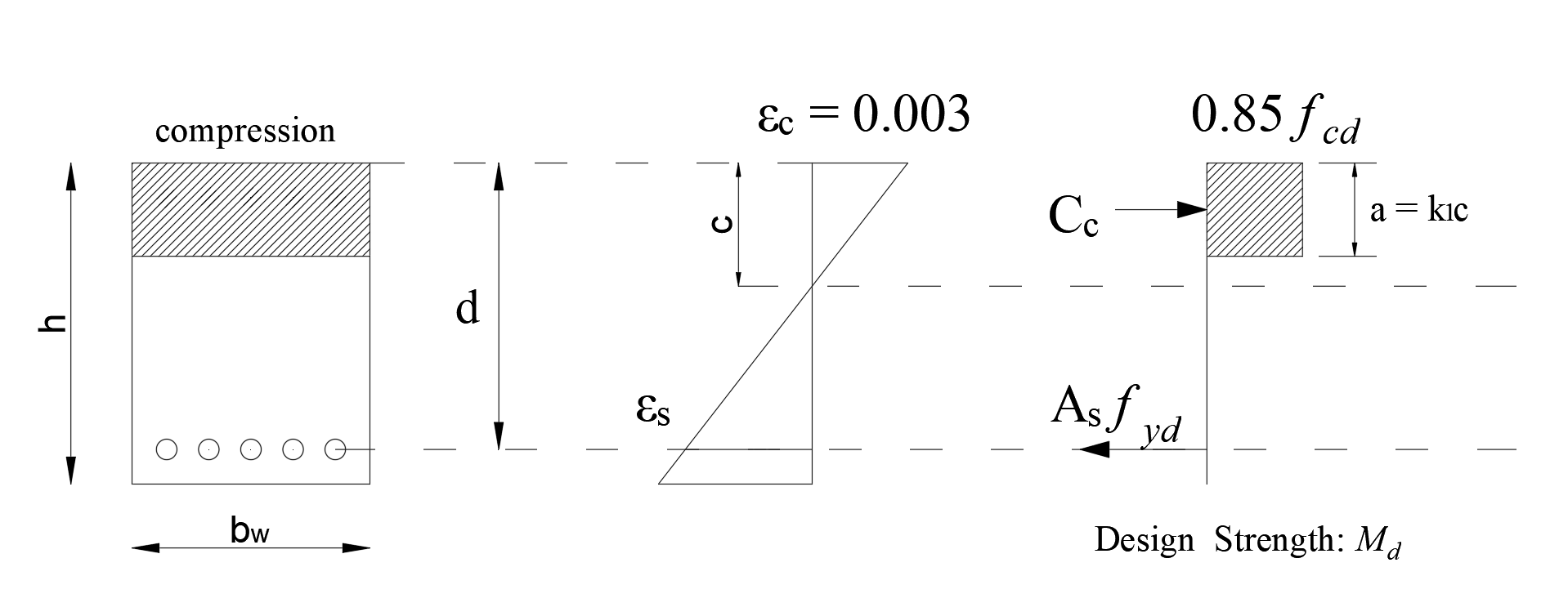
The total forces C_c and C_s resulting from the stresses of concrete and reinforcement are shown below.

From the equation of equilibrium:

Nominal flexural strength M_n:

or

Next Topic

TSC Axial strength or Combined Flexural and Axial Strength

Related Topics

• TSC One-Way Shear Strength

• TSC Torsional Strength