Punching Shear Check Example 1

Punching Shear Design Example

In the example calculation, a punching calculation will be made for a column whose dimensions are 100x80. Other parameters in the calculation are listed as follows.

• Slab thickness: 27 cm

• Slab cover: 3 cm

• Material : C35/S420

• f_ctd = 1380.42 kN/m² (Concrete design tensile strength)

Download ideCAD for ACI 318-19 with Punching Shear Check

• Structural Design Software, including Punching Shear

The slab useful height, d , is calculated;

d = ( Slab thickness - Slab cover ) = 27 - 3 = 24 cm

Column dimensions

c₁ = 100 cm c₂ = 80 cm

The punching circumference (u_p) is calculated at a distance d/2 from the column surface and is shown in the picture below. In this case, punching is done by adding d to the column dimensions to find the perimeter's edges (b1, b2).

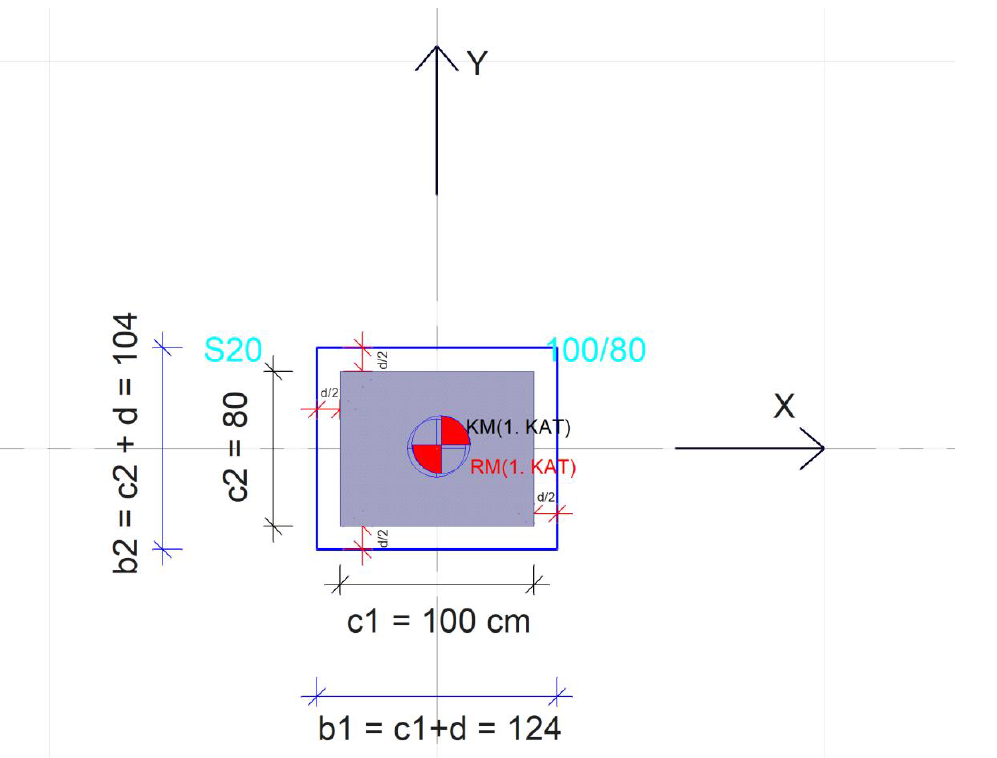
In this case, the punching circumference (u_p ) and the punching area (A_z) obtained by multiplying the punching perimeter by the flooring useful height, d, is calculated as shown below.

The shear stresses plotted below are the punching stresses perpendicular to the slab plane.

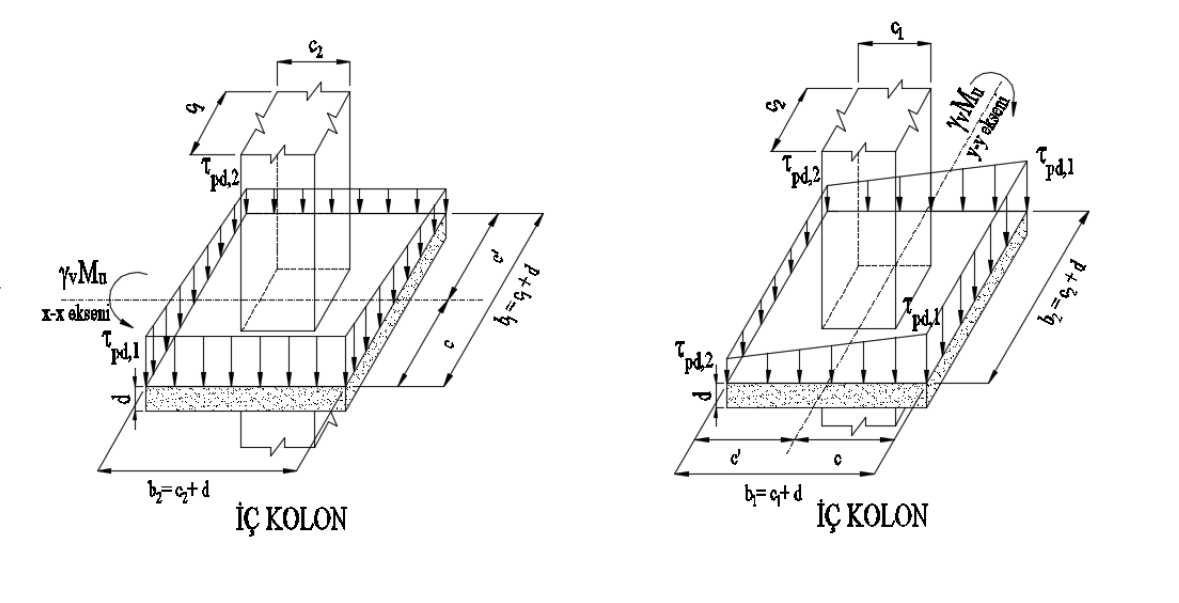
The J values ​​are the sum of the polar inertia and second moments of inertia of the surfaces forming the punching area (A_z). TBDY Equation 7.28 calculates this value according to the loading direction considering the γ_f coefficient.

Calculation of J and γ_f Coefficients for Strong Axis (Major Direction)

The coefficients γ_f(maj) and γ_v(maj) are calculated as follows.

The following operations are performed to find the J (maj) value.

c _(maj) is the center of gravity distance perpendicular to the moment vector, which is considered when finding the J value ( J _(maj) ) on the strong axis of the section. Since the punching circumference is rectangular,

The polar inertia and second moments of inertia are calculated as follows, respectively.

In this case, the sum of the polar inertia and second moments of inertia about the section's strong (major) axis, J _(maj), is found as follows.

Calculation of J and γ_f Coefficients for Weak Axis ( Minor Direction )

The following steps are followed to calculate the γ _f(min) and γ _v(min) coefficients.

The J_(min) value is found as follows.

The c_(min) value is the center of gravity distance perpendicular to the moment vector, which is considered when finding the J value (J _(min)) on the weak axis of the section. Since the punching circumference is rectangular,

In this case, the polar and second moments of inertia are found as follows, respectively.

In this case, the sum of the polar inertia and second moments of inertia about the section's weak (minor) axis, J _(min), is found as follows.

Finding Punching Stresses

The forces to be considered for punching stresses and the values ​​obtained from the hand geometry are given below.

• V_d = 683.13 kN

• DM _d(maj) = 143.53 kNm

• DM _d(min) = 546.65 kNm

• A_z = 1.0944 m ²

• γ_f(maj) = 0.579

• γ_v(maj) = 0.421

• γ_f(min) = 0.621

• γ_v(min) = 0.379

• J_(maj) = 0.27101448 m ⁴

• J_(min) = 0.2083328 m ⁴

• c_(maj) = 0.62 m

• c_(min) = 0.52m

• c'_(maj) = 0.62 m

• c'_(min) = 0.52 m

The punching stresses are found by substituting all the above values ​​in the stress formulas and the internal forces essential to the punching design.

The absolute value of τ _pd,1 , τ _{pd,2 is τ pd,1} = 1279.56 kN/m ² . This obtained value is compared with the f_ctd value, which is the concrete design tensile strength.

τ_pd,1 = 1279.56 kN/m² < f_ctd = 1380.42 kN/m²

Upholstery punching strength is sufficient. These values ​​can also be compared with the report results.

Punching Shear Design Software

ideCAD Structural is an All-in-One Structural Engineering Software with Punching Shear Design and many other Structural Design Code Check tools.

Download ideCAD for ACI 318-19 with Punching Shear

• Free Reinforced Concrete Design Software