Steel Beam Design Example

Design strength check of the steel beam named PL019 is done under the most unfavorable internal forces as a result of general analysis determined according to TBDY 2018 9.3.1.4. The material and section information of the beam is as follows:

Steel material: S275 F_y =275 N/mm ² F_u =430 N/mm ²

Cross section: IPE 450

I_x= 33740 cm⁴	I_y= 1676 cm⁴	J_x= 66.87 cm⁴	C_w= 791000 cm⁶
W_ex= 1500 cm³	W_px= 1702 cm³	A= 98.80 cm⁴
d=450 mm	h=378.8 mm	b_f= 190 mm	t_f= 14.6 mm
t_w=9.4 mm	i_x=184.8 mm	i_y=41.2 mm

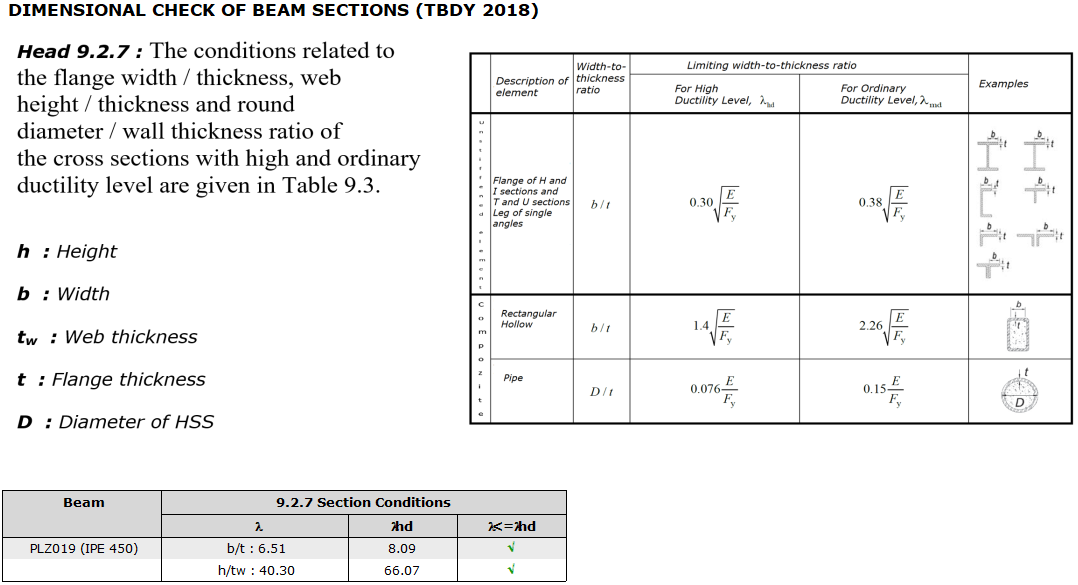
Control of Cross Section Conditions (TBDY 9.3.1)

It should be checked whether the flange width/thickness and web height/thickness values of the beam cross-section exceed λ_hd value given in Table 9.3 .

Cross section flange;

koşulu sağlar.

Cross-section web;

The result of the analysis was accepted as 0 because the axial force value was low.

koşulu sağlar.

The control of the cross-section conditions is done according to TBDY 2018 Table 9.3 in the steel beam report and summarized in tabular form.

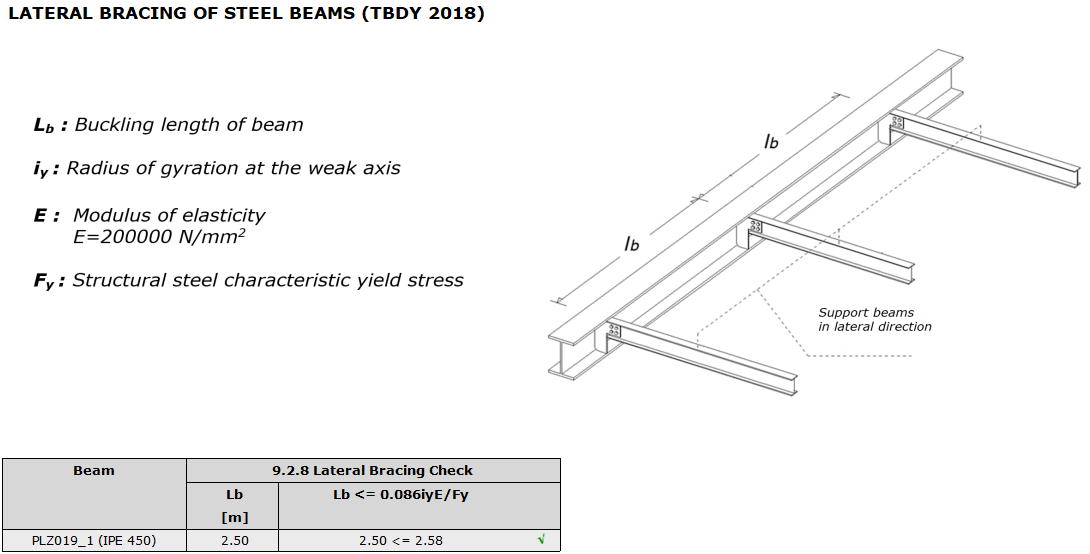
Lateral Supporting of Beam Flange

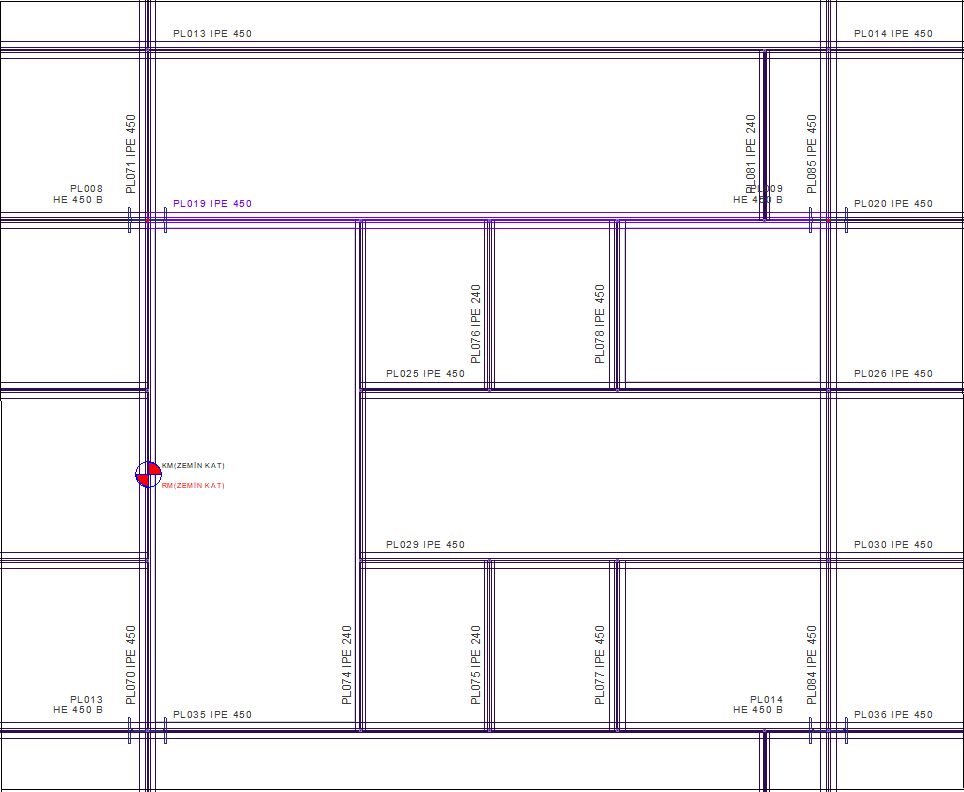
The longest unsupported beam segment in the lateral direction is L_b = 2.0 m. According to TBDY 2018 9.2.8.1(a), the distance between the points where the lower and upper ends of special beams are supported, L_b should meet the following condition.

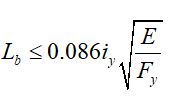
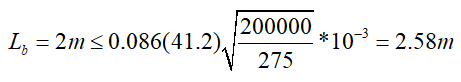
It provides the condition. In the steel beam report, the control results are given in tables.

Flexural Moment Strength

While checking the beam design flexural moment strength, since the lateral supported lengths are different, station-by-station should be done for each section. For the convenience of manual check, it will be done for the section L_b = 0.75 m, which is exposed to the most unfavorable flexural moment.

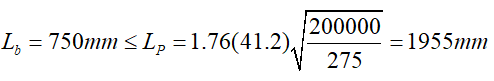
Because of the condition, the characteristic of flexural moment strength is determined according to yield limit condition. According to the CYTHYE equation 9.2, the check is done as follows:

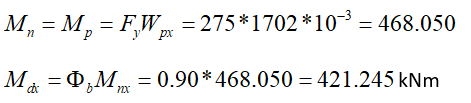
As a result of the analysis, the required flexural moment strength obtained as a result of 1.2G+Q-Ex-0.3Ey+0.2S+0.3Ez loading is M_u = 203.637 kNm.

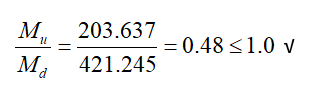
Shear Strength of The Beam

According to ÇYTHYE 10.2.1(a) in I-cross section with double symmetry axes,

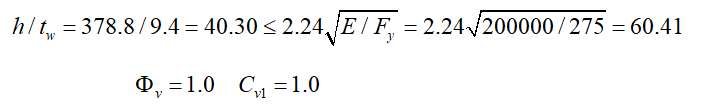
With the load combination Q-Ex-0.3ey + 1.2G + 0.2S + 0.3ez, required shear force is determined as V_u = 12818 kN. It has been shown above that the cross-sectional capacity is sufficient.

Next Topic

Strong Column - Weak Beam Control