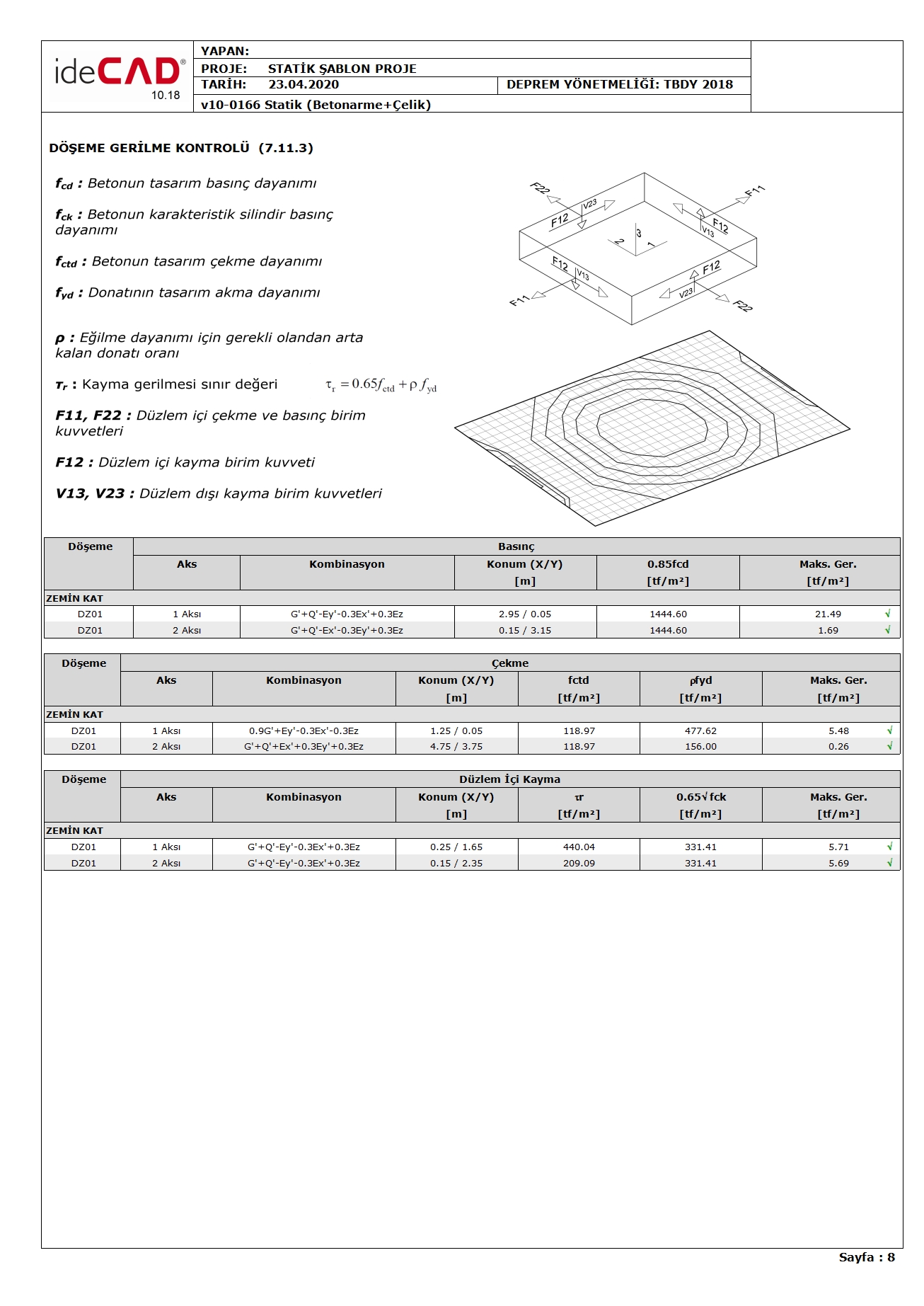
(7.11.3) Example
In the sample project, the in-plane pressure, tensile and shear stress control will be made in the D01 slab according to the conditions specified in Article 7.11.3 of TBDY.
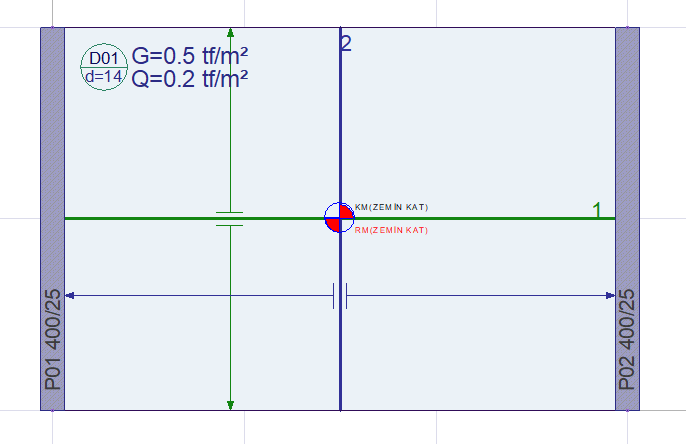
Material: C25 / S420
Design compressive strength of concrete, f cd = 25 / 1.5 = 16.67 MPa = 1699.867 tf / m 2
Design tensile stress of concrete, f ctd = 1.167 MPa = 118.97 tf / m 2
Reinforcement design yield strength, f yd = 420 / 1.15 = 365.22 MPa = 37242.076 tf / m 2
Strength Excess Coefficient, D = 2.5
Slab thickness, d = 14 cm = 0.14 m
Pressure Stress Control
The solution will be made under the effect of the G '+ Q'-Ey'-0.3Ex' + 0.3Ez load combination obtained from the semi-rigid diaphragm solution. The highest stress value caused by the earthquake load Ey 'in the negative direction of the slab is at the lower midpoint of the slab. In this case, F11 values on axis 1 at this point are as follows.
G'=-0.683 tf/m Q'=-0.272 tf/m Ex'=0.00077 tf/m Ey'=0.814 tf/m Ez'=-0.3 tf/m
In this case, taking into account the strength excess coefficient, the value of F11 formed at the G '+ Q'-Ey'-0.3Ex' + 0.3Ez load combination is as follows.
F11 = (-0.683) + (-0.272) - 2.5(0.814 + 0.3*0.00077) + 0.3(-0.3) = -3.08 tf/m
found as. Compressive stress that occurs,
F11/d = 3.08/0.14 = -22.00 tf/m2
found as. According to Article 7.11.3 of TBDY , this value must be less than 0.85f cd .
0.85f cd = 0.85 * 1699.867 = 1444.60 tf / m 2 > 22.00 tf / m 2 Condition is met .
Tensile Stress Control
The solution will be made under the effect of the 0.9G '+ Ey'-0.3Ex'-0.3Ez load combination obtained from the semi-rigid diaphragm solution. The F11 value calculated by considering the strength excess coefficient was read as 0.7672. The compressive stress that occurs in this case,
F11/d = 0.7672/0.14 = 5.48 tf/m2
found as. According to Article 7.11.3 of TBDY , if this value exceeds f ctd, the yield strength of the remaining reinforcement required for the flexural strength of the said stress should not exceed ρf yd .

Since the calculation is made on the slab 1 axis, the reinforcements on this axis will meet the stress in the F11 direction. There is 14/20 reinforcement placement on the reinforcement axis number 1, with flat reinforcement at the top and bottom. The sum of the top and bottom bars for a length of 1 m is 12. Ratio of reinforcement in 1 m length,
Reinforcement of 1m length = π * (14 2 /4) * 12 = 1847.256 mm 2 / m = 18:47 cm 2 / m
The reinforcement required for bending strength is 1.02 cm 2 / m
In this case, the ratio of reinforcement remaining from the required for bending strength is ρ,
p = (18.47-1.02) / (14 * 100) = 0.0125
ρfyd = 0.0125 * 37242.076 = 464.20 tf/m2
is happening. The condition is satisfied since the stress value is 5.48 <f ctd = 118.97 tf / m 2 .
In-Plane Shear Stress Control
The solution will be made under the effect of the G '+ Q'-Ey'-0.3Ex' + 0.3Ez load combination obtained from the semi-rigid diaphragm solution. The F12 value calculated by considering the strength excess coefficient was read as 0.81. In this case the in-plane shear stress,
F12 / d = 0.81 / 0.14 = 5.78 tf / m 2 . According to Article 7.11.3 of TBDY , in-plane shear stress shall not exceed the limit value given by Equation 7.25 .
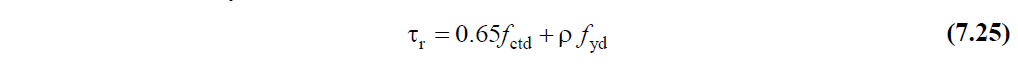
Since calculations were made in 1 slab calculation axis, the area of reinforcement (14/20) on this axis was found to be 18.47 cm 2 for 1 m length . The reinforcement required for bending strength was read as 5 cm 2 / m in an area close to the curtain edge . In this case, the ratio of reinforcement remaining from the required for flexural strength is ρ,
ρ = (18.47-5.00) / (14 * 100) = 0.00962
τ r = 0.65f ctd + ρf yd = 0.65 * 118.97 + 0.00962 * 37242.076 = 435.72 tf / m 2 .
According to Article 7.11.3 of TBDY, the in -plane shear stress should not exceed 0.65 (f ck ) 1/2 . In this case
0.65(fck)1/2 = 0.65*(25)1/2 = 3.25 MPa = 331.41 tf/m2
The condition was fulfilled since the in -plane shear stress value was 5.78 tf / m 2 <435.72 tf / m 2 and 5.78 tf / m 2 <331.41 tf / m 2 .