Minimum Flexural Strength of Columns per ACI 318-19 with ideCAD

How does ideCAD control the minimum flexural strength of columns according to ACI 318-19?

• For special moment frames, minimum flexural strength of columns are calculated automatically, aacording to ACI 18.7.3.

Notation

A_g = gross area of concrete section, in²
f_c^' = specified compressive strength of concrete, psi
f_y = specified yield strength for nonprestressed reinforcement, psi
M_n = nominal flexural strength at section, in.-lb
M_nb = nominal flexural strength of beam including slab where in tension, framing into joint, in.-lb
M_nc = nominal flexural strength of column framing into joint, calculated for factored axial force, consistent with the direction of lateral forces considered, resulting in lowest flexural strength in.-lb
M_pr = probable flexural strength of members, with or without axial load, determined using the properties of the member at joint faces assuming a tensile stress in the longitudinal bars of at leasts 1.25f_y and a strength reduction factor ϕ of 1.0, in.-lb
P_u = factored axial force; to be taken as positive for compression and negative for tension, lb
ϕ = strength reduction factor

The columns of special moment frames are considered as part of the seismic-force resisting system. The subject of this title is to reduce the possibility of yielding in columns of special moment frames. Columns not stronger than beams increased the likelihood of inelastic action. The worst possible case is when all columns in a given story have flexural yielding at both ends. In this case, it creates a column failure mechanism to cause collapse. In order to avoid this situation, the minimum flexural strength of column control given in ACI 18.7.3 should be satisfied.

The flexural strengths of the columns shall satisfy ACI Eq.(18.7.3.2),

ΣM_nc is the sum of nominal flexural strengths of columns framing into the joint. Column flexural strength is calculated for the factored axial load, P_u, consistent with the direction of the lateral forces considered, resulting in the lowest flexural strength.

ΣM_nb is the sum of nominal flexural strengths of the beams framing into the joint, evaluated at the faces of the joint.

The obtaining of ΣM_nc and ΣM_nb values are shown below for both directions.

• ΣM_nc = M_n4 + M_n3

• ΣM_nb = M_n2 + M_n1

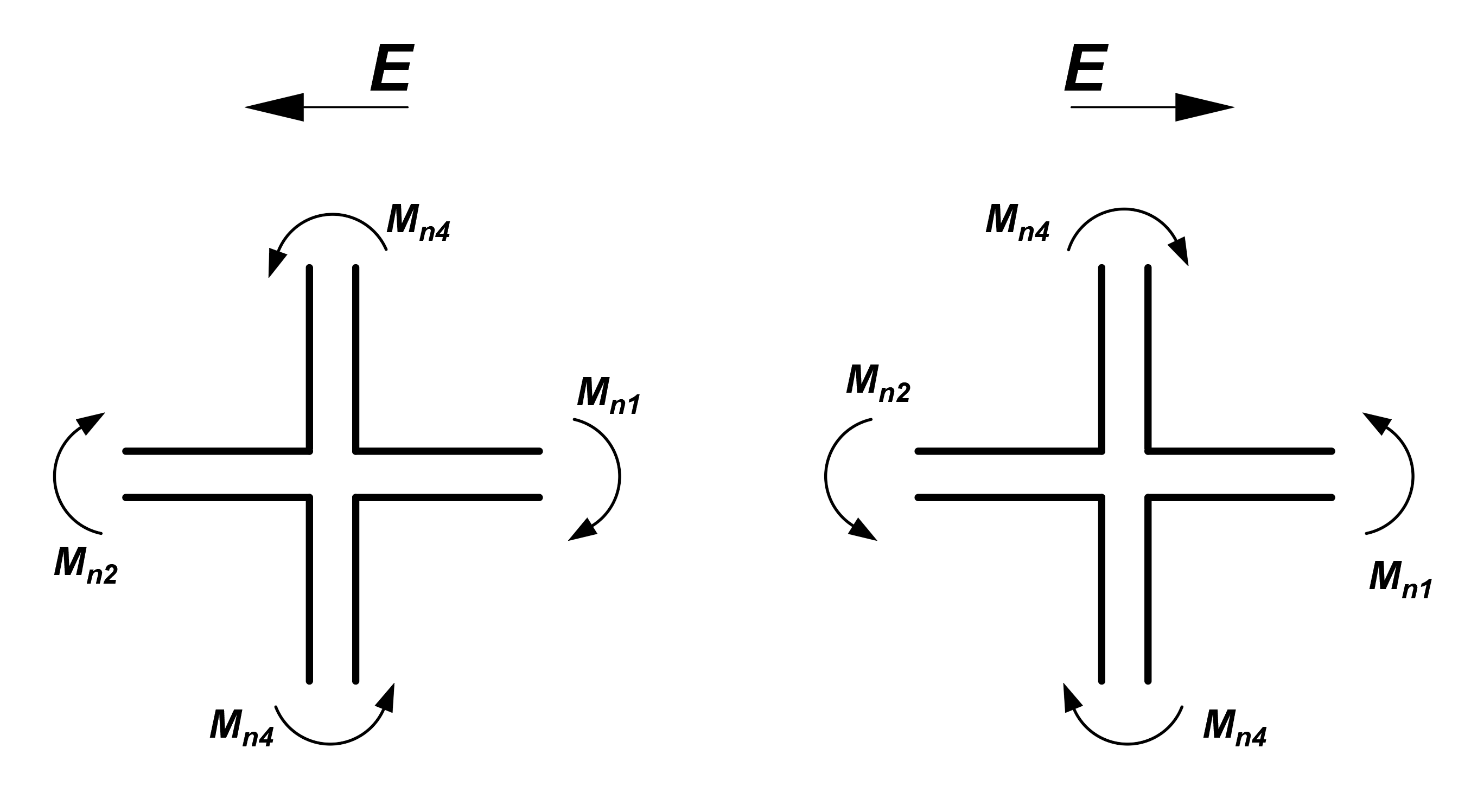
The factored axial force, P_u, in each column is calculated from the program for each load combination. For each design load combination, the moment capacity of each column under the unfilence of axial load is then determined separately for the major and minor directions of the column, using the three-dimensional interaction failure surface.

The M_n values used in the calculation of ΣM_nc and ΣM_nb values are the nominal flexural strengths described in the Flexural Strength per ACI 318-19 with ideCAD and Axial strength or Combined Flexural and Axial Strength per ACI 318-19 with ideCAD titles. Nominal flexural strength M_n is calculated without using the strength reduction factor (ϕ=1) and as the reinforcement yield stress f_y. M_n is shown by the green curve in the graph above.

Columns should satisfy ACI Eq.(18.7.3.2), except for the two cases given below.

• Connections where the column is discontinuous above the connection.

• Column factored axial compressive force, P_u under load combination including earthquake effect, E are less than A_gf_c^' /10.

Next Topic

Column Reinforcement Limits per ACI 318-19 with ideCAD

Related Topics

• Column Combined Flexural and Axial Design per ACI 318-19 with ideCAD

• Column Shear Design per ACI 318-19 with ideCAD

• Reinforced Concrete Column Design Limits per ACI 318-19 with ideCAD

• Column Reinforcement Limits per ACI 318-19 with ideCAD

• Column Reinforcement Detailing per ACI 318-19 with ideCAD