Use of Different R and D Coefficients for Upper and Lower Pats of Structures with Basement
Symbols
D | Strength Excess Coefficient |
D alt | Strength Excess Coefficient applied to the lower part of the building |
D üst | Strength Excess Coefficient applied to the lower part of the building |
R | Carrier System Behavior Coefficient |
R alt | Structural System Behavior Coefficient applied to the lower part of the building |
(R a ) alt | Earthquake Load Reduction Coefficient applied to the lower part of the building |
(R a ) n, alt | Earthquake Load Reduction Coefficient applied to the lower part of the building in nth vibration mode |
R üst | Structural System Behavior Coefficient applied to the lower part of the building |
( R a ) üst | Earthquake Load Reduction Coefficient applied to the upper part of the building |
(R a ) n, üst | Earthquake Load Reduction Coefficient applied to the upper part of the building in the nth vibration mode |
T | Natural vibration period |
Tn | Natural vibration period of the nth mode |
Tp(X) | (X) the dominant natural vibration period of the building in the direction of the earthquake |
νn(X) | The coefficient used in the calculation of the equivalent earthquake load reduction coefficient applied in the nth mode for the lower part of the building |
ν alt (X) | Coefficient used to calculate the reduced internal forces caused by the vibration of the lower part of the building itself |
ν n, alt(X) | Coefficient used to calculate the reduced internal forces from the vibration of the lower part of the building itself in the nth mode |
νüst(X) | Coefficient used to calculate the internal forces transferred from the upper to the lower part of the building |
ν n, üst(X) | Coefficient used to calculate the internal forces transferred from the upper to the lower part of the building in the nth mode |
4.3.6. Using Different R and D Coefficients in Upper and Lower Sections of Buildings
In buildings where different R and D coefficients are used in the upper and lower sections , calculations will be made according to the rules given in 4.3.6.1 or 4.3.6.2 . According to the definition given in 3.3.1 , these rules can also be applied in buildings with basements surrounded by rigid walls. Alternatively, calculations can be made according to the rules described in 4.7.5 or 4.8.5 .
With the Equivalent Earthquake Load Method explained in 4.3.6.1 - 4.7 , in the calculation made by considering the entire carrier system ( upper section + lower section );
(a) the top section wherein the structural elements corresponding to the ductility internal forces reduced to upper table (4.1) from the selected R top and the D top coefficients and considering the received (X) the natural vibration period prevails in the earthquake direction T p (X ) 'e substituted by Eq. (4.1) from the calculated Seismic Load Reduction Factor (R a ) top will be obtained using.
(b) The reduced internal forces corresponding to the non-ductile behavior of the carrier system elements in the upper section will be obtained by multiplying the internal forces obtained in (a) with the upper coefficient D.
(c) The equivalent earthquake load reduction coefficient (R a ) for reduced internal forces corresponding to the ductile behavior of the structural system elements in the subsection shall be determined by Sub Equation (4.4) :
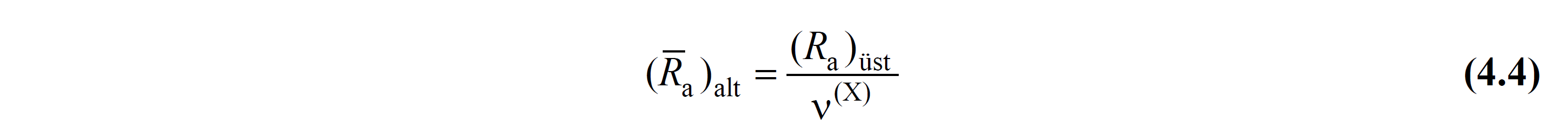
The coefficient ν (X) in this equation is given below:
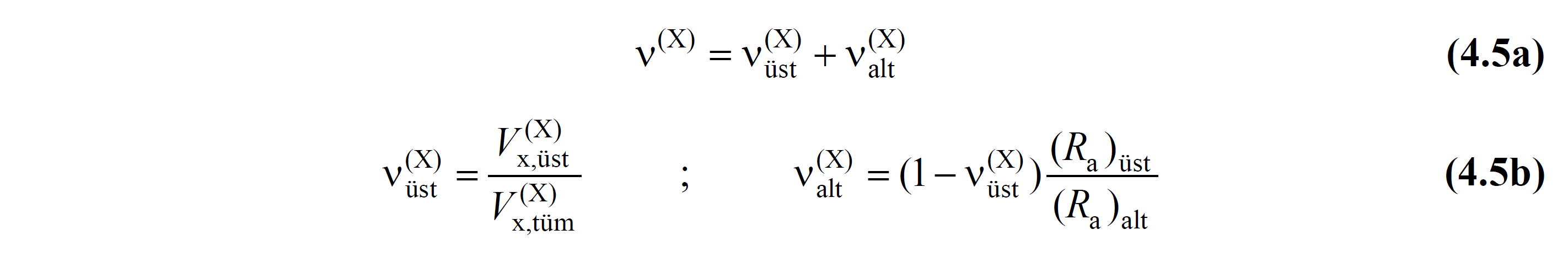
Eq. (4.5 A) 'in the first term ν top (X) , the upper portion from the lower portion ' E transmitted reduced forces, the second term (X) ν lower (X) The subsection 'to calculate the reduced forces generated by its own vibration corresponds to the coefficients used. Seismic Load Reduction Coefficient calculated from Equation (4.1) depending on R sub and D sub- coefficients selected from Table (4.1) and T p (X) for the carrier system in sub- subsection (R a ) It shows. ν top (X) is defined as the ratio of the base shear force of the upper section to the base shear of the entire load-bearing system ( upper section + lower section ) under unabated seismic loads .
(d) The reduced internal forces corresponding to the non-ductile behavior of the structural system elements in the subsection shall be obtained by multiplying the internal forces obtained in (c) by the equivalent strength excess coefficient defined below :
:d_czg_alt:
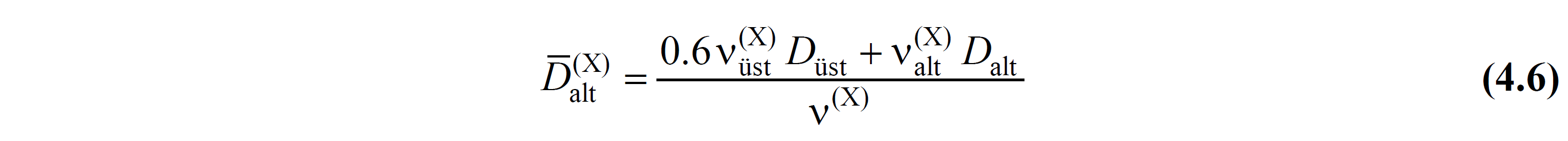
With the Modal Calculation Methods explained in 4.3.6.2 - 4.8 , the calculation made by considering the entire carrier system ( upper section + lower section ),
(a) All operations in Equation (4.4), Equation (4.5) and Equation (4.6) shall be applied for each n th vibration mode and taking into account the relevant natural vibration period T n . In the nth mode , instead of the ratio of base shear forces in Equation (4.5b) , the ratio of modal effective masses corresponding to these shear forces in the same mode can also be used (See 4B.1.4 ).
(b) R is lower <R top in rigid basement systems which, for all modes of Eq. (4.5b) from the ν n, parent (X) 'in case of avoiding to calculate always gives less favorable results ν n, parent (X) = 0 can be assumed. In this case, the following simplifications can be made for the subdivision in the n'th mode:
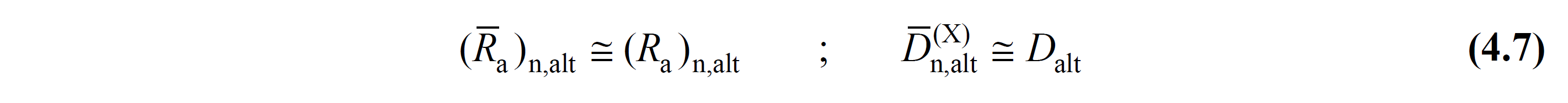
D sub = 1.5 for basements according to 4.3.2.3 .
Related Topics
