Castellated Beam Design per AISC 360-16

How does ideCAD design castellated beams according to AISC 360-16?

• Castellated steel beam design is made automatically according to AISC 360-16.

• The user can change steel beam design settings.

Symbols

C_b : The lateral-torsional buckling modification factor
Z_x = Plastic section modulus about the x-axis, in.³ (mm³)
E: Modulus of elasticity of steel = 29,000 ksi (200 000 MPa)
F_y : Specified minimum yield stress of the type of steel being used, ksi
F_cr : Critical stress
K : Effective length factor
L: Laterally unbraced length of the member
P_r: Required axial force resistance for LRFD or ASD load combinations
P_c: Strength of axial compressive force available according to Section E
M_r: Required bending moment strength for LRFD or ASD load combinations
M_c: current bending moment strength according to Section F
r: Radius of gyration
λ: Width-to-thickness ratio for the element as defined in Section B4.1
λ_r : Limiting width-to-thickness ratio as defined in Table B4.1a
L_b : Length between points that are either braced against lateral displacement of the compression flange or braced against twist of the cross-section, in. (mm)
L_p : The limiting laterally unbraced length for the limit state of yielding, in. (mm)
L_r : The limiting unbraced length for the limit state of inelastic lateral-torsional buckling, in. (mm),
M_n : The nominal flexural strength
M_p : Plastic bending moment
S_x : Elastic section modulus taken about the x-axis, in.³ (mm³)

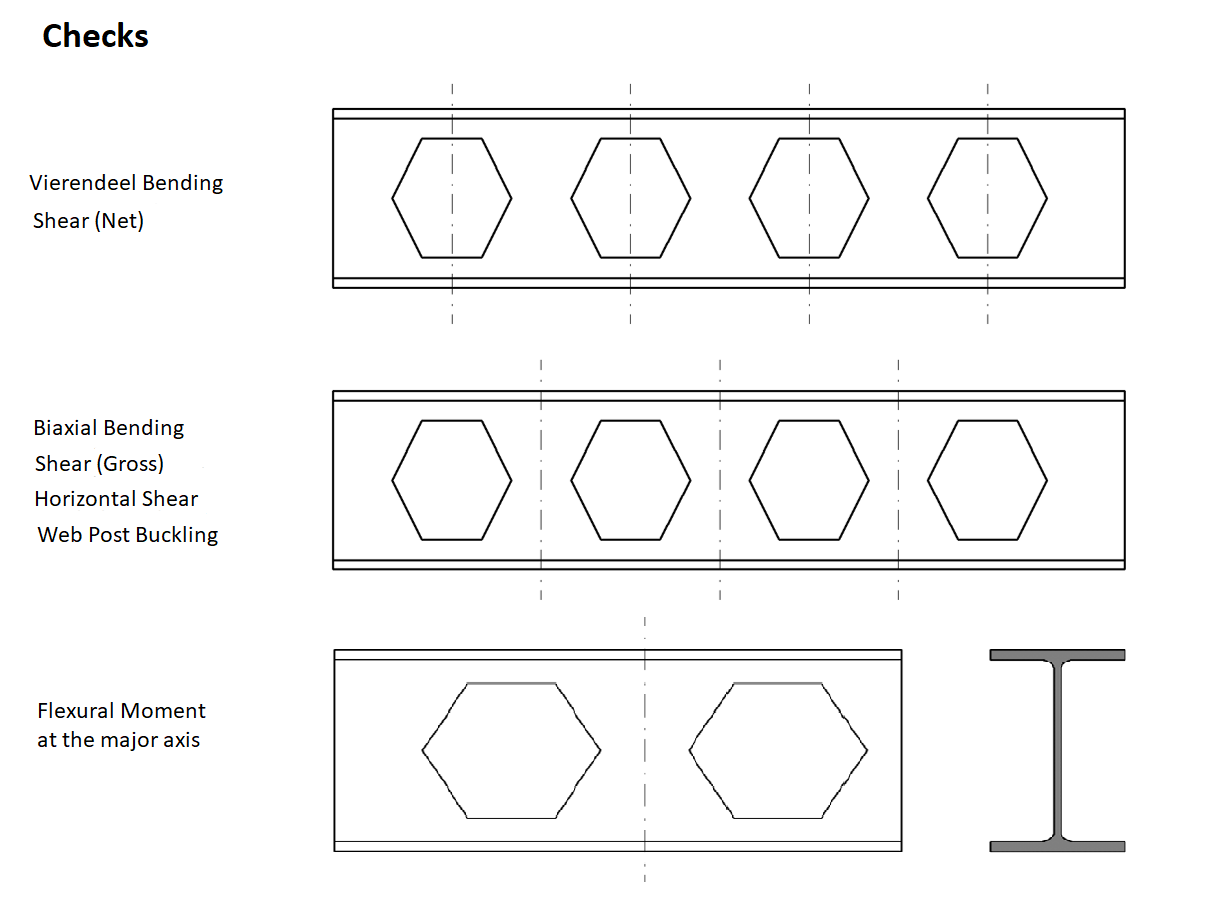
Castellated Beam Sections

Castellated hexagonal, castellated circular, castellated octagonal, and angelina sections can be defined. Castellated hexagonal and castellated circular sections are designed.

Biaxial Bending and Axial Force

Yielding Limit State

For the yield limit state, the nominal flexural strength, M_n, is calculated using the equation below by AISC 360-16.

• When L_b ≤ L_p

• When L_p < L_b ≤ L_r

• When L_b > L_r

Axial Force

The axial compression capacity for the web part of the castellated beam is calculated as follows.

The critical stress, F_cr, is calculated as shown below.

• When

• When

Combined Forces

Equation H1.1 is used for biaxial and single symmetry axis members under combined axial compression and flexural moment.

Shear Control

Gross and Net Area Shear Control

Shear control with the gross area is the full web part of the castellated beam, while the shear control with the net area is calculated by considering the castellated beam's hollow section.

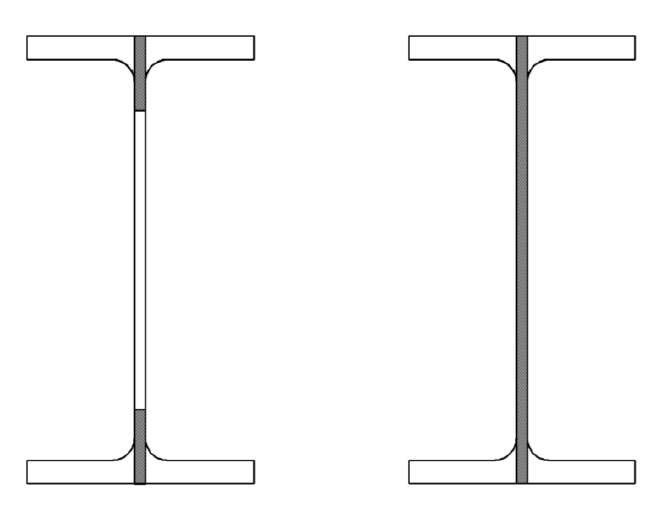
Horizontal Shear Control

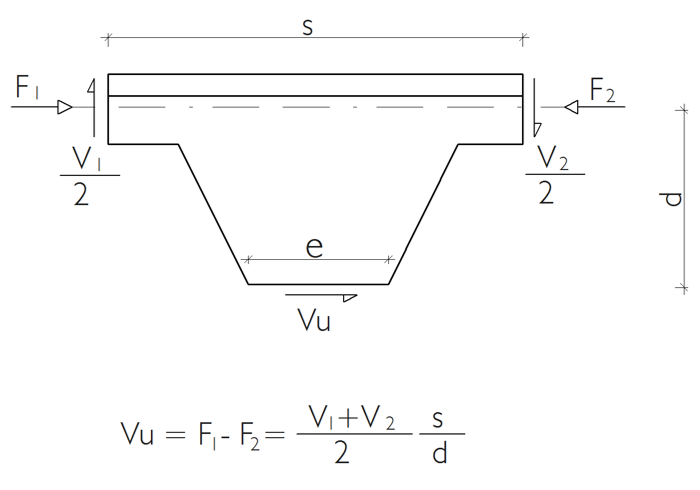
The shear force on the castellated beam web is calculated using the balance equation and compared with the shear strength.

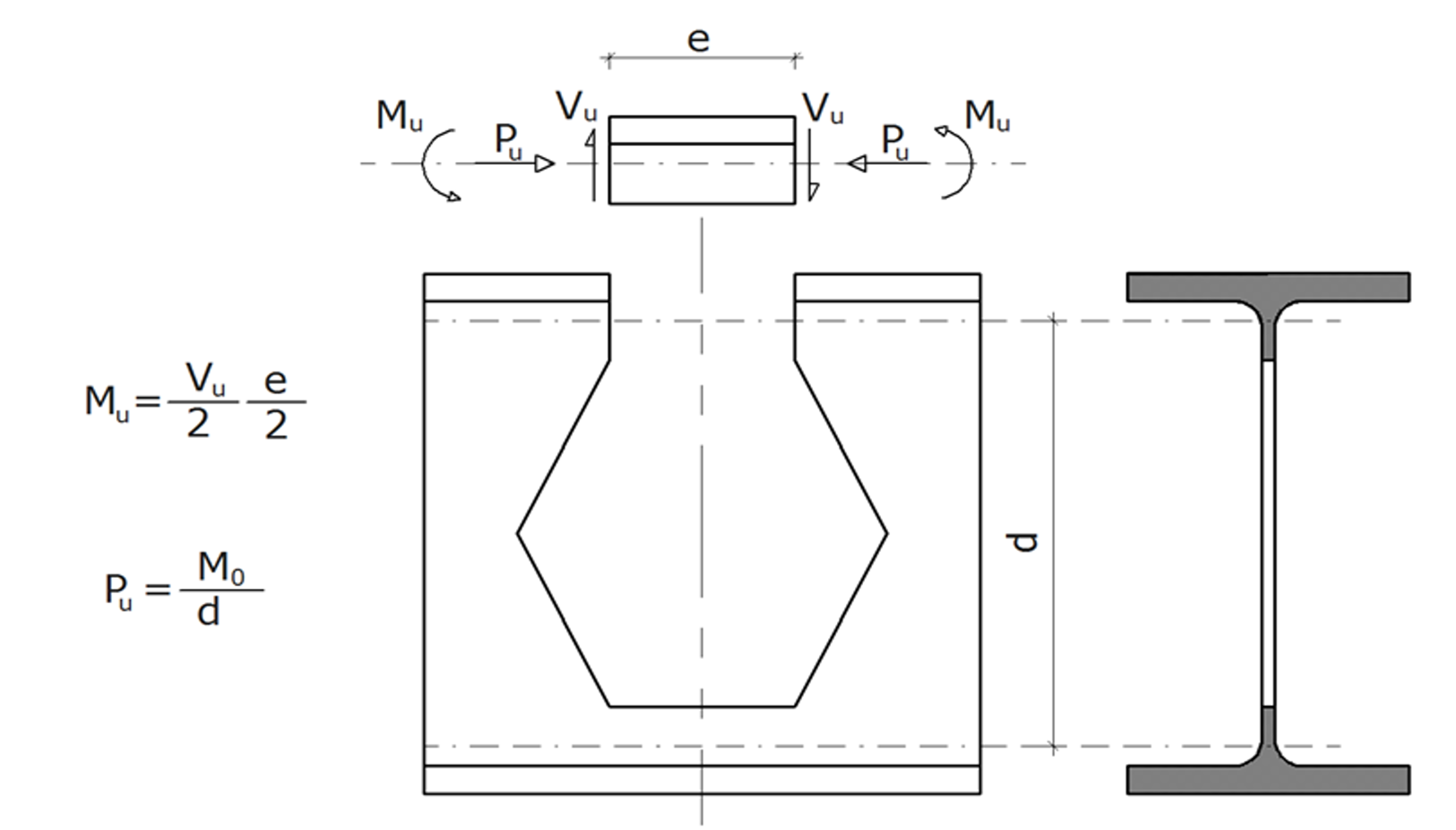
Vierendeel Bending Control

Axial Force and Biaxial Bending

The effects of the T section on the castellated beam spaces are found with the equilibrium equation. Internal force diagrams are used in the static analysis while calculating these forces. The equation of equilibrium calculates the bending moment and axial force on the T section. Then, the combined effects are considered by calculating the T-section bending and axial force strengths.

Web Post Buckling Control

Forces Acting on the Web

The bending moment values ​​at the upper and lower boundaries of the web section between the castellated beam spaces are found, and lateral-torsional buckling is checked according to the rectangular section.

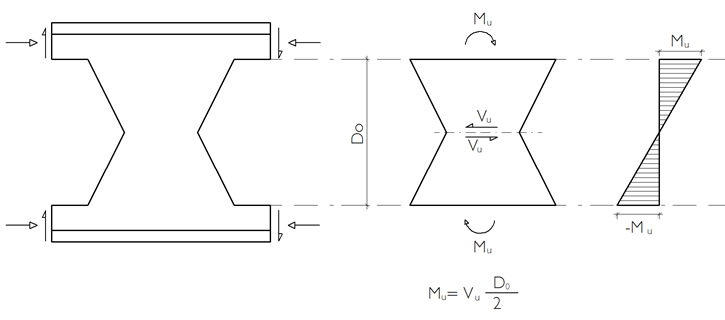
Web Post Buckling Strength

The web section between the castellated beam is calculated according to AISC 360-16 Section F.

• The limit state of flange local buckling does not apply to sections with compact flanges.

• The nominal flexural strength, M_n, is calculated below for sections with noncompact flanges.

• The nominal flexural strength, M_n, is calculated below for sections with slender flanges.

Next Topic

Castellated Beam Example with AISC 360-16

Related Topics

• Steel Beam Design Settings

• Steel Beam Design per AISC 360-16

• Composite Beams with Steel Headed Stud Design per AISC 360-16

• Crane Beam Design per AISC 360-16