Structure Mass
Based on the structure geometry, element cross-sectional dimensions and external loads present in the building, the weight of the structure will be calculated in terms of force for each element using the formulas below and the total structure weight will be calculated by adding all of them. It will then compare it with the program.
Element's Weight (force) = Element's Volume (volume) * Element's UnitVolume Weight (force / volume)
Weight (force) = Areaload (force / area) * Area of the element (area)
Weight (force) = Linear Load (force / length) * Element's Length (length)
Typical floor plan view and dimensions of a 3-storey building:
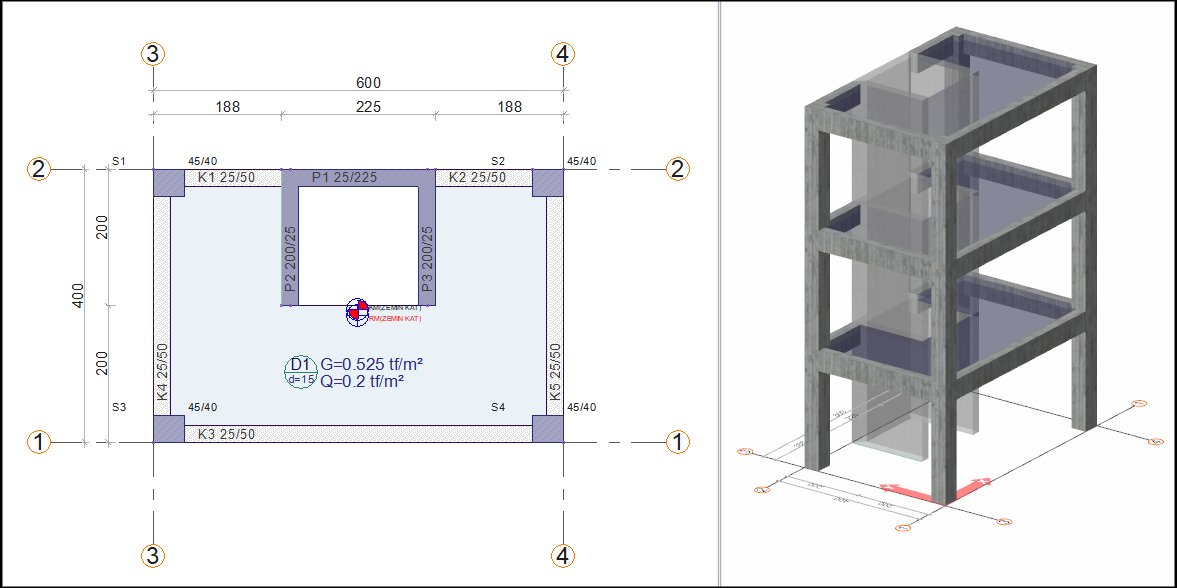
Data
Columns dimensions = 45/40 cm
Beam dimensions = 25/50 cm
Group curtain total length = 6 m
Group curtain thickness = 0.25 m
Slab thickness = 15 cm
Floor covering weight = 0.15 tf / m2
Slab moving load weight = 0.200 tf / m2
Floor area = 15.193 m2 (can be measured with the area command)
Floor height = 3 m
Wall height = 3 - 0.5 = 2.5 m
13 cm brick, 0.25 tf / m3 was used in all beams.
Wall weight for 1 meter = 0.25 tf / m3 = 0.25 * 2.5 = 0.625 tf / m
Concrete core weight (reinforced concrete) = 2.5 tf / m3
Live load participation coefficient n = 0.3 at all floors
Beam clean deficits:
K1 = 142.5 cm
K2 = 142.5 cm
K3 = 510 cm
K4= 320 cm
K5 = 320 cm
Column height = 300 cm
Calculation of floor weight for a floor
Beam self weights
K1-> 1.425*2.5*0.25*0.50 = 0.445
K2-> 1.425*2.5*0.25*0.50 = 0.445
K3-> 5.10*2.5*0.25*0.50 = 1.593 tf
K4-> 3.20*2.5*0.25*0.50 = 1.0 tf
K5-> 3.20*2.5*0.25*0.50 = 1.0 tf
Total = 4.483 tf
Column self weights
Sum for 4 columns (S1, S2, S3, S4) → 0.40 * 0.45 * 3 * 2.5 * 4 = 5.4 tf
Group Curtain self weight
6*2,5*3*0.25 =11.25 tf
Slab self weight
→ D1 = 15.193 * 2.5 * 0.15 5.69
Total Self-Weight = 4.483 + 5.4 + 11.25 + 5.69 = 26.823 tf
Wall loads
K1 → 1.425*0.625 = 0.89 tf
K2 → 1.425*0.625 = 0.89 tf
K3 → 5.10 * 0.625 = 3.1875
K4 → 3.20*0.625 = 2 tf
K5 → 3.20*0.625 = 2 tf
TotalWall = 8.9675 tf
Floor covering load
→ D1 = 15.193 * 0.15 2.279
Ground Floor Total Fixed Load Weight G
G = 2.279 +8.9675+26.823
G= 38.07 tf
Floating Load Weight Q
D1 tile → 0.200 * 15.193 = 3.038
Q=10.386 tf
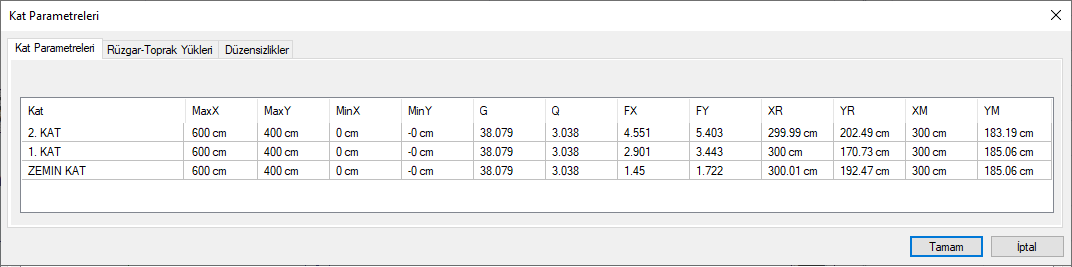
G and Q values calculated by the program for each floor can be seen in floor parameters .
Total structure weight
W = G+ n*Q
W Zeminkat = 38.07 + 0.3 * 3.38 = 38.99 tf
W 1st floor = 38.07 + 0.3 * 3.38 = 38.99 tf
W 2nd floor = 38.07 + 0.3 * 3.38 = 38.99 tf
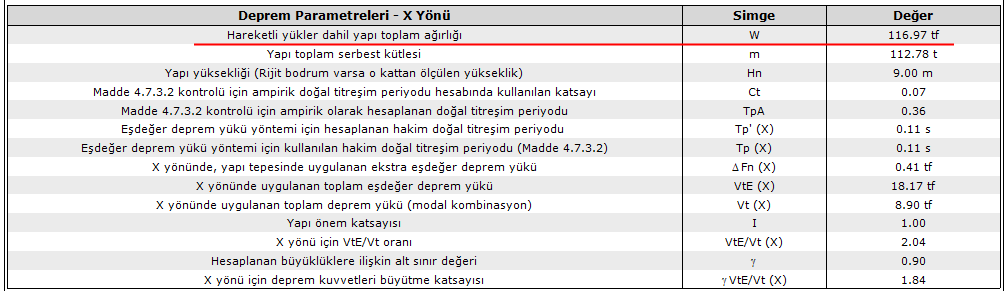
W toplam = 116.97 tf
The total weight of the structure can be seen in the dynamic analysis report.
Calculation of the mass due to the diaphragm in the walls
It is half the sum of the joints of finite elements belonging to the joints connected to the rigid diaphragm in shell elements. It is the grayscale portion of finite elements marked with an X in the figure.
A single curtain is chosen for the numerical example and a single slab for a rigid diaphragm has been chosen.
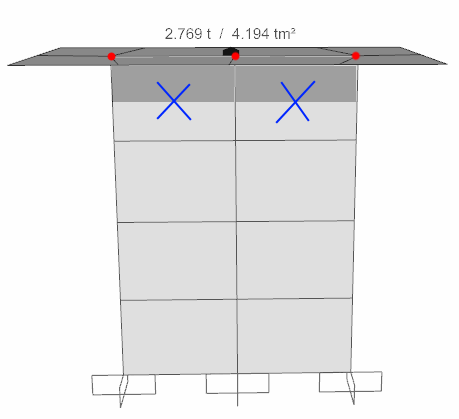
Floor thickness is 12 cm, there is no covering, live load is entered as zero. The floor area is 7,531 m2.
The curtain size is 25/218. The floor height is 3 meters.
Curtain self-weight = 25 * 218 * 2.5 * 3 = 4.0875 tf
A network is formed with 8 finite elements in the curtain.
The weight of the single finite element is = 4.0875 / 8 = 0.51 tf.
The curtain is connected to the rigid diaphragm by 2 finite elements with 3 joints. Half of the masses of the finite elements attached to the rigid diaphragm is the mass of the curtain attached to the rigid diaphragm.
Curtain mass = 0.51 * 2/2 = 0.51 tf
The entire flooring is involved.
0.12 * 2.5 * 7.531 = 2.259
The rigid diaphragm has mass = 0.51 + 2.259 = 2.769 tf.
Calculation of free mass in walls

Half of the sum of the masses of finite elements belonging to the joints attached to the foundation in shell elements is not included in the free mass.
Curtain weight = 25 * 218 * 2.5 * 3 = 4.0875 tf
Weight of slab = 0.12 * 2.5 * 7.531 = 2.259
Total weight w = 4.0875 + 2.259 = 6.36465 tf
A network is formed with 8 finite elements in the curtain.
The weight of the single finite element is = 4.0875 / 8 = 0.51 tf.
Curtain 2 is grounded in a finite element
The curtain held mass is = 0.51 * 2/2 = 0.51 tf
Free mass of curtain = 4.0875-0.51 = 3.5775
Total free mass of the structure = 3.5775 + 2.259 = 5.83 tf
Calculation of the mass attached to the diaphragm in columns
In the columns, it is half the weight of the columns attached to the rigid diaphragm. (It is the part toned with dark gray in the figure.)
Single column for numerical example and single slab for rigid diaphragm were selected.
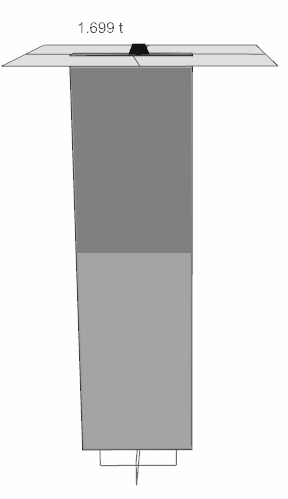
Floor thickness is 12 cm, there is no covering, live load is entered as zero. Floor area is 3 m2.
The column size is 25/85. The floor height is 3 meters.
Column self-weight = 0.25 * 0.85 * 2.5 * 3 = 1.593 tf
Weight of tile = 0.12 * 2.5 * 3 = 0.9
The mass attached to the rigid diaphragm is half the weight of the column
Column mass = 1.593 / 2 = 0.796 tf
The entire flooring is involved.
The rigid diaphragm has mass = 0.79 + 0.9 = 1.69 tf.
Calculation of free mass in columns

Column self-weight = 0.25 * 0.85 * 2.5 * 3 = 1.593 tf
Weight of tile = 0.12 * 2.5 * 3 = 0.9
Total weight w = 1.593 + 0.9 = 2.5 tf
The mass attached to the rigid diaphragm is half the weight of the column
Column serbets mass = 1.593 / 2 = 0.796 tf
Total free mass of the structure = 0.9 + 0.796 = 1.70 tf
