Reinforcement Material Model
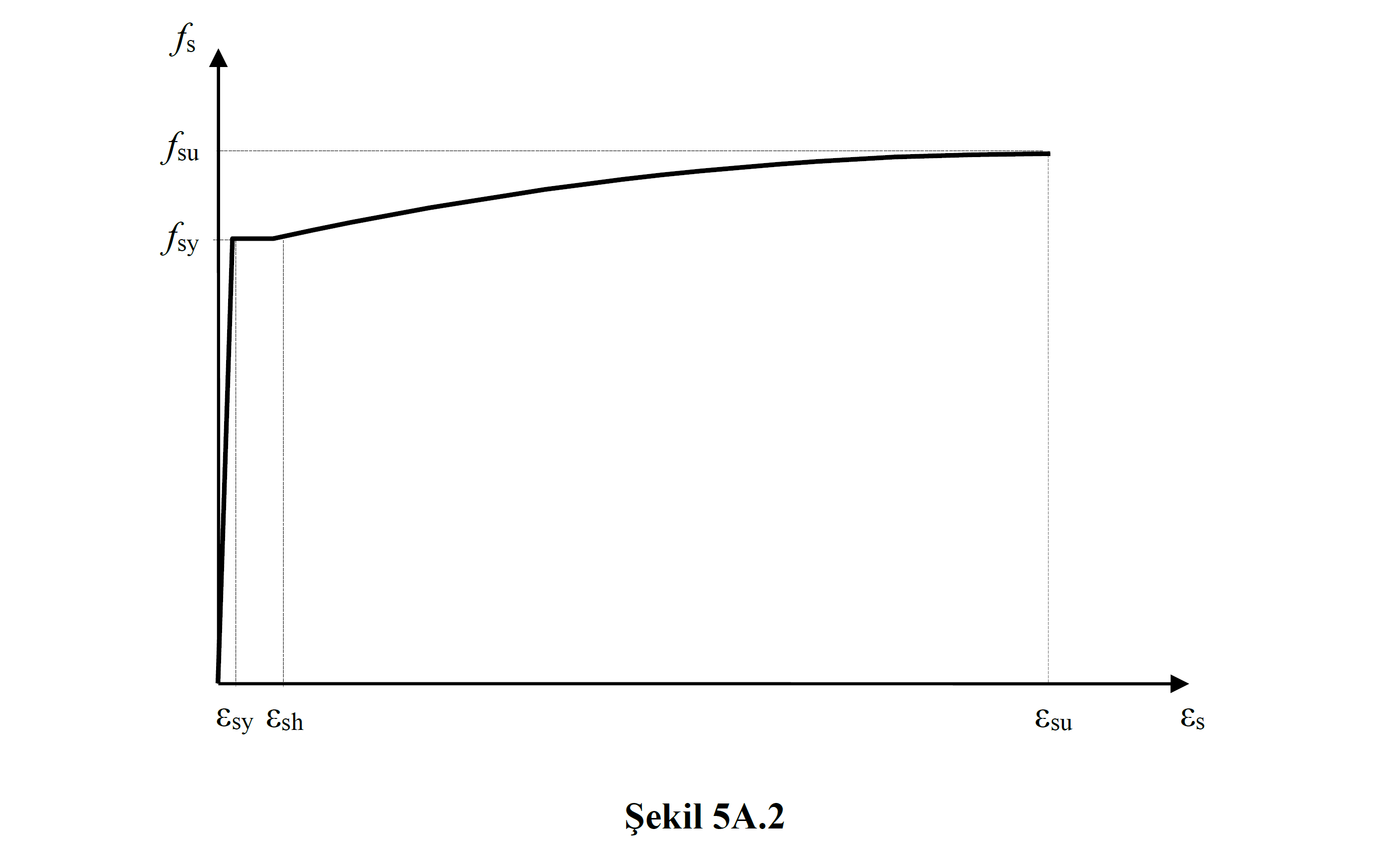
The material model to be used in the evaluation according to the deformation of the reinforcement steel model determined by the user is automatically calculated according to Figure 5A.2.
ICONS
E s = Modulus of elasticity of reinforcement steel
f s = Stress in reinforcement steel
f sy = Yield strength of reinforcement steel
f su = Tensile strength of reinforcement steel
f yw = Yield strength of transverse reinforcement
f yk = Characteristic yield strength of reinforcement steel
ε s = Strain of reinforcement steel
ε sy = Yield strain of reinforcing steel
ε sh = Unit deformation of reinforcement steel at the beginning of hardening
ε water = rupture strain of reinforcement steel
In Annex 5A.2 of TBDY Section , the stress strain relations for the reinforcement steel model are explained and shown in Figure 5A.2 .
The relation required to obtain the above graph is shown in Equation (5A.7) .
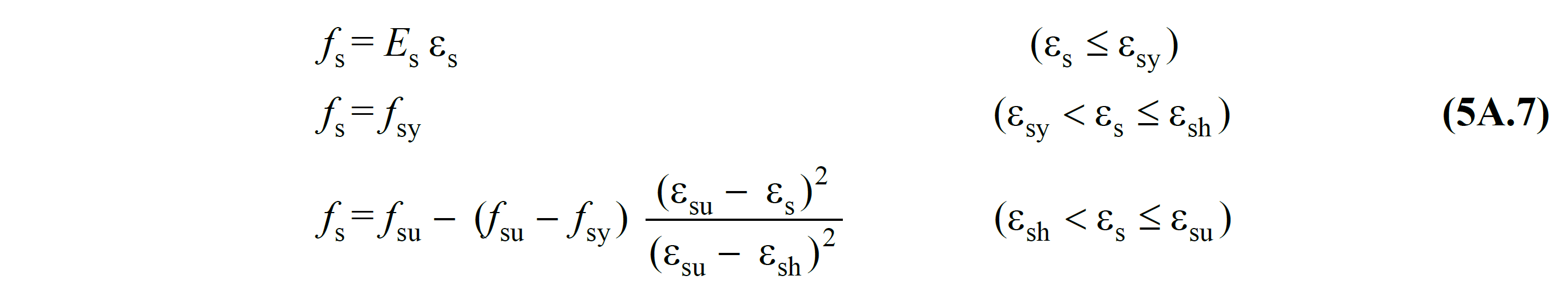
In this equation, f s represents the stress of reinforcement steel and is the vertical axis of the graph in Figure 5A.2 . ε s is the unit strain of reinforcing steel and represents the horizontal axis of the graph. The section up to the yield stress f sy of the reinforcement is linear and no plastic deformation occurs until this section. After reaching the yield point (f sy , ε sy ) of the reinforcement, the stress remains constant and the unit deformation increases until the hardening zone. Hardening starting point (f sy , ε sh ) is an amount of increase continues after the tension in the reinforcement and finally (f water , ε waterAt the point), the reinforcement loses its strength. Depending on the quality of the reinforcement steel, the yield stress f sy and the yield strain sy vary. Table 5A.1 shows the values used in the material model according to the reinforcement quality.
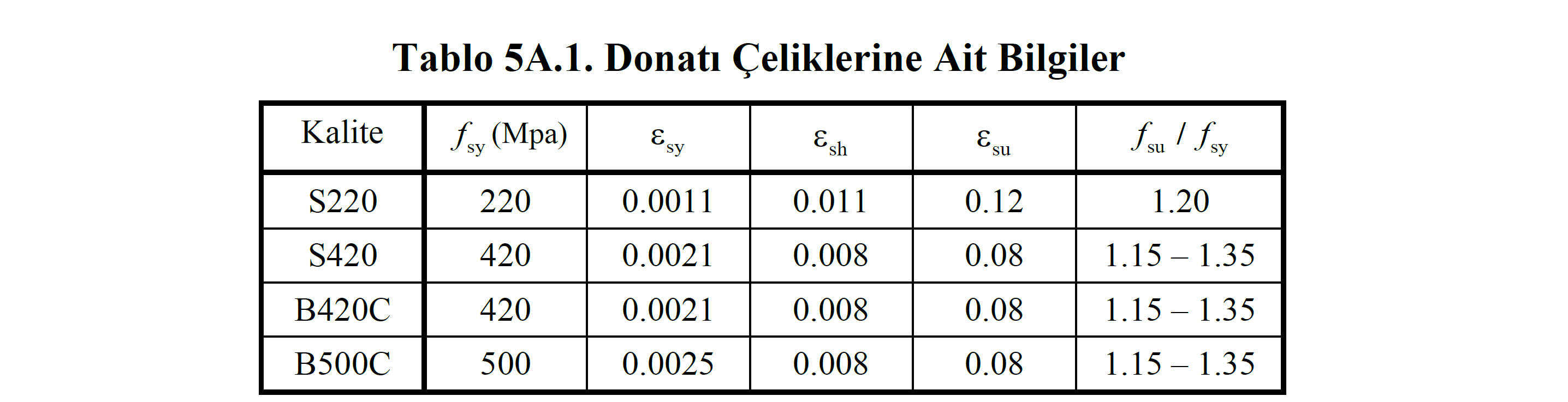
The characteristic of f yk reinforcement steel is the yield strength. While creating the material model for new buildings, the reinforcement yield stress f sy should be calculated with the expected (average) strength . In this case , it is considered as f sy = 1.3f yk . In case existing structures are evaluated, the existing material strength is used. If the knowledge level is selected as "Comprehensive", the reinforcement yield stress is taken as f sy = f yk , if the knowledge level is selected as "Limited", f sy = 0.75f yk .
For example, for a reinforcement of S420 quality, the characteristic yield strength is f yk = 420 MPa. If this reinforcement is to be used in the ŞGDT approach for an existing structure and the information level is selected as "comprehensive", the reinforcement yield stress used in defining the plastic joint is f sy = f yk = 420 MPa. However, if the ŞGDT approach is used in a new structure, the reinforcement yield stress used in defining the plastic joint is f sy = 1.2f yk = 504 MPa.
Next Topic
