Modal Characteristics and Lateral Load İncrement Determination (5B.2.1 , 5B.2.2)
Modal characteristics of each thrust step TDY Appendix 4B from the modal contribution Multiplier Base Shear mode shape and modal effective mass is calculated automatically.
ICONS
a 1 (X,k) = modal pseudo-acceleration of the first mode modal single degree of freedom system at the kth push step for the earthquake direction [m/s 2 ]
d 1 (X,k) = (X) modal displacement of the modal single degree of freedom system belonging to the first mode at the kth push step for the earthquake direction [m]
m i = i th floor total mass
m ix1 (X,k) = (X) each i th floor modal effective mass [t]
m iy1 (X,k) calculated according to the variable mode shape renewed with the free vibration calculation in a kth thrust step
= (X) ith floor modal effective mass calculated according to the variable mode shape renewed with the free vibration calculation at each kth thrust step in the x axis direction for the earthquake direction[t]
m iθ1 (X,k) ) = (X) ith floor modal effective mass moment of inertia calculated according to the variable mode shape regenerated by the free vibration calculation at each kth thrust step in the x axis direction for the earthquake direction[tm2]
Δa 1 (X,k) = (X) modal pseudo-acceleration[m/s2] of the modal one degree of freedom system belonging to the first mode at the kth push step for the earthquake direction
Δf ix1 (X,k) = (X) earthquake load increase acting in the x axis direction at the i th floor at the k th push step for the earthquake direction [kN]
Δf iy1 (X,k) = (X) earthquake direction k ' Earthquake load increase acting in the y-axis direction at the i th floor in the th push step [kN]
Δf iθ1 (X,k) = (X) earthquake load increase acting in the z axis direction at the i th floor at the k th push step for the earthquake direction [kN]
Φ ix1 (k) = the amplitude of the variable mode shape in the x direction, which is renewed with the free vibration calculation at each kth thrust step at the i'th floor
Φ iy1 (k) =the amplitude of the variable mode shape in the y direction renewed with the free vibration calculation at each kth pushing step at the i'th floor
Φ iθ1 (k) = The amplitude of the variable mode shape in the z direction, which is renewed with the free vibration calculation at each kth thrust step at the i-th floor
Γ 1 (X,k) = (X) modal contribution factor calculated according to the variable mode shape renewed with the free vibration calculation at each kth thrust step for the earthquake direction
In the Adaptive Single Mode Pushover Analysis Method , the earthquake load increments acting on the floors in the direction of the considered earthquake and the floor displacement increments compatible with them , the variable mode shape obtained from the modal analysis done by considering the plastic hinges formed in the previous steps in each push step after the initial step . calculated proportionally. In the initial step of the thrust analysis, nonlinear incremental static calculation results are obtained, taking into account the second-order effects under non-earthquake loadings . In this method , modal capacitance diagram whose coordinates are modal displacement-modal pseudo-acceleration without drawing the thrust curve is obtained directly.
While applying the Variable Single Mode Repulsion Method , the internal forces and strains, which take into account the second-order effects of non-earthquake loadings, are taken into account as the initial value (0 th step). As stated in TDY 5B2.1 , the seismic load increments acting on the floors in the (X) earthquake direction considered in the Variable Single Mode Repulsion Method are calculated at each k th thrust step after the initial step (0 th step) where the non-earthquake loadings are taken into account. The variable mode shape obtained as a result of the modal analysis reconstructed taking into account the change in stiffness caused by the plastic hinges 'how it is calculated. The earthquake load increments calculated in the x,y,z direction for the earthquake direction (X) considered ; Δf ix1 (X, k) , Δf iy1 (X, k) and Δf iθ1 (X, k) , times the effective modal mass in terms TBDY Equation 5B.7 'is calculated as shown.
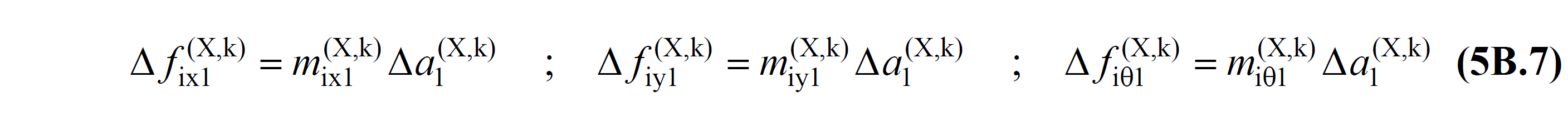
In this equation, m ix1 (X,k) , m iy1 (X,k) and m iθ1 (X,k) are calculated according to the mode shape obtained from the free vibration calculation (modal analysis) made at each kth thrust step. are modal effective masses . The values of m ix1 (X,k) , m iy1 (X,k) and m iθ1 (X,k) are determined by TBDY Equation 5B with modal calculation methods , taking into account the varying stiffness matrix in the formation of plastic hinges at each push step depending on the free vibration mode It is calculated as shown in .8 .
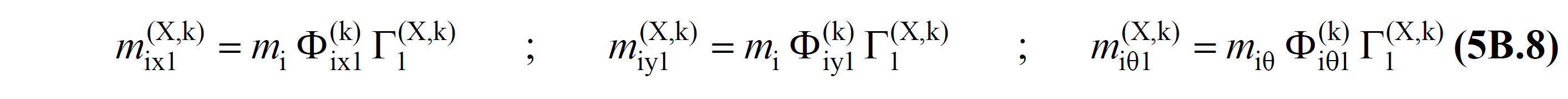
TDY Equation 5B.8 from the m ix1 (X, k) , m iy1 (X, k) and m iθ1 (X, k) values, each k in the kth pushing step, that step in which, depending on the shape of the free vibration mode refreshed TBDY is the first mode (dominant mode) equivalent of the effective masses calculated in Equation 4B.2 given in Annex 4B . Φ ix1 (k) , Φ iy1 (k) and Φ iθ1 (k)Mass Definition at Joints (5.4.6) modeled as described in the title.
The term Δa 1 (X,k) specified in TDY Equation 5B.7 is the modal pseudo-acceleration increment of the modal single degree -of- freedom system belonging to the first mode as a result of the modal analysis performed at each kth push step for the (X) earthquake direction . is. The modal pseudo-acceleration increment is calculated from the yield condition of the new plastic hinge(s) resulting from the k - th step .
Variable Single Mode Jacking Method 'n Constant Single Mode Pushover Analysis Method ' from the most important difference between, seismic load increments ' s plastic deformation result of the structure due to each Considering from displacements and stiffness changes k 'modal analysis in th thrust step' s repeated Building Modal Its characteristics are found by recalculating . While there are m ix1 (X,k) , m iy1 (X,k) and m iθ1 (X,k) values in the Constant Single Mode Pushover Analysis Method, the results obtained as a result of the modal analysis in the first step (k=1) performed only after the initial step. Φ ix1(k) , Φ iy1 (k) , Φ iθ1 (k) and Γ 1 (X,k) values are used. In this case, k=1 for these terms in each pushing step, and the stiffness change in the case of the plastic hinge is not taken into account. However Variable Single Mode Jacking Method ' n, each k after the start step nd repeated modal analysis in step push and earthquake load increments at every step, again performed as a result of modal analysis calculated Φ ix1 (k) , Φ iy1 (k) , Φ iθ1 (k ) and Γ1 (X,k) values are used. For this reason , the Variable Single Mode Propulsion Method gives more realistic results inbuildings where second order effects may be significant. TDY 5B.1.6 at vertical load of the second-order effects caused by the conveyor system stopped şekildeğiş's buildings may be important to Fixed Mode Jacking Method in the bottom because it is based on shearing forces, these effects can not be compatible format into account, 5B.2 from the It is recommended to use the Variable Mode Push Method .
