A Simply Supported Beam

Calculate by hand the deformation of joint 2 of the following simple beam using the Virtual Work Method.

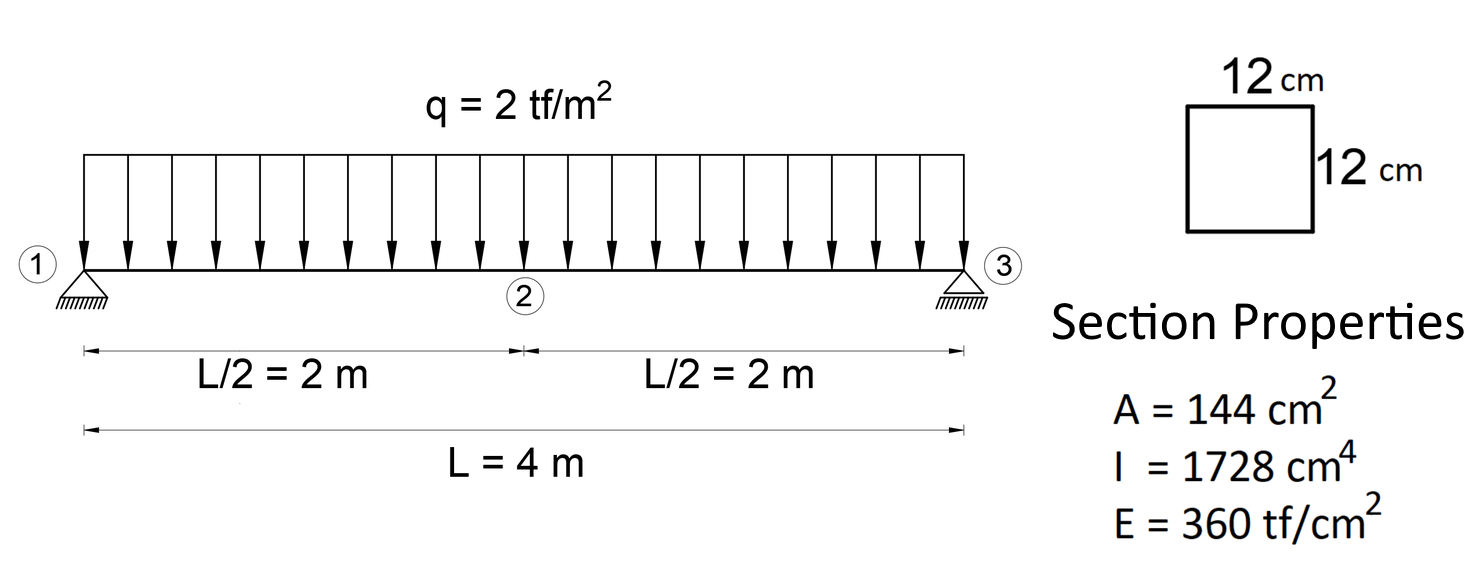
Hint for solution

According to the method; the integral should be considered separately for the bars between 1-2 and 2-3 nodes.

Detailed solution

E= Modulus of elasticity A= Cross-sectional area I= Cross-section moment of inertia

M= Moment due to external loading M'= Moment due to unit loading Δ= Deformation

Step 1 Finding Moment function by Unit Loading

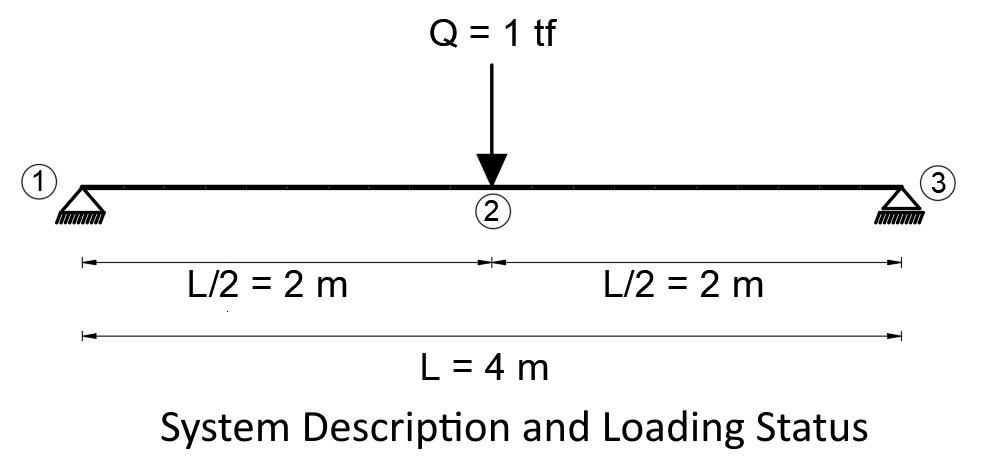
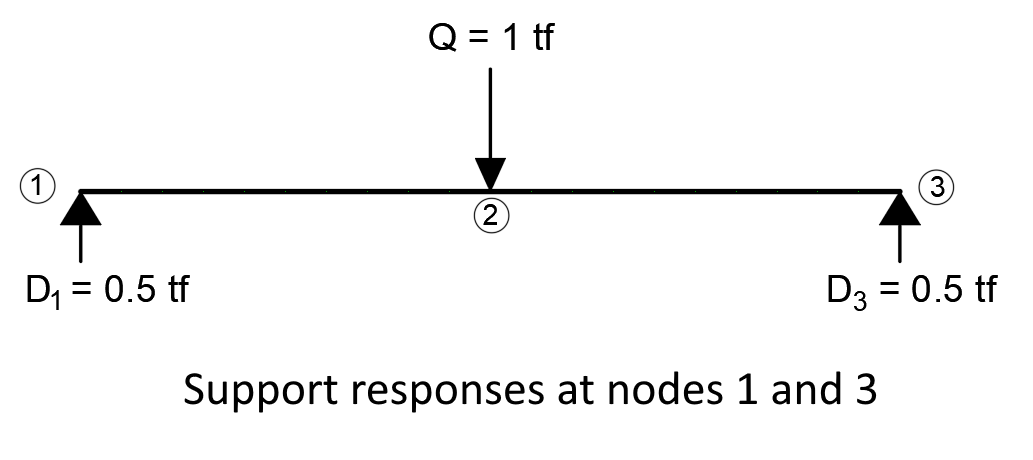
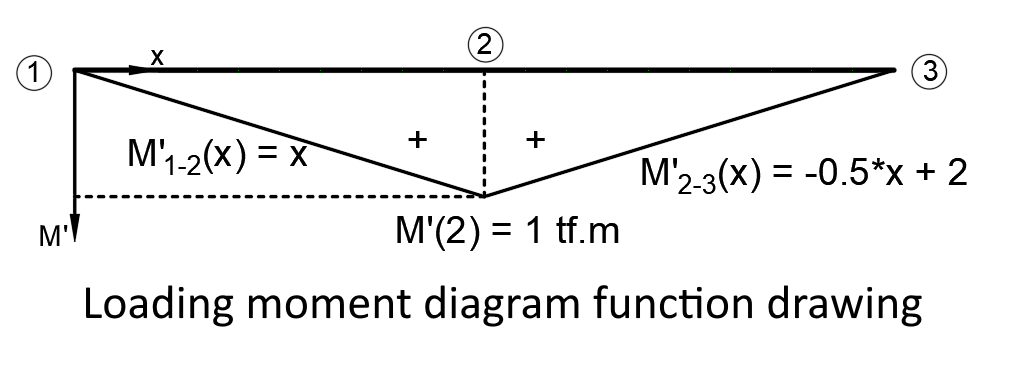
Q: unit load D₁ , D₃ : Support responses M'(2): 2 DN moment value L: Element length

M'_1-2 (x): 1-2 Moment function M_2-3 (x): 2- 3 Moment function ΣM_1,dn: Total moment relative to 1 DN.
ΣD: Total balance

Moment Function 1-2 :

Moment Function 2-3 :

Step 2: Finding the Moment Function Based on the Given Load

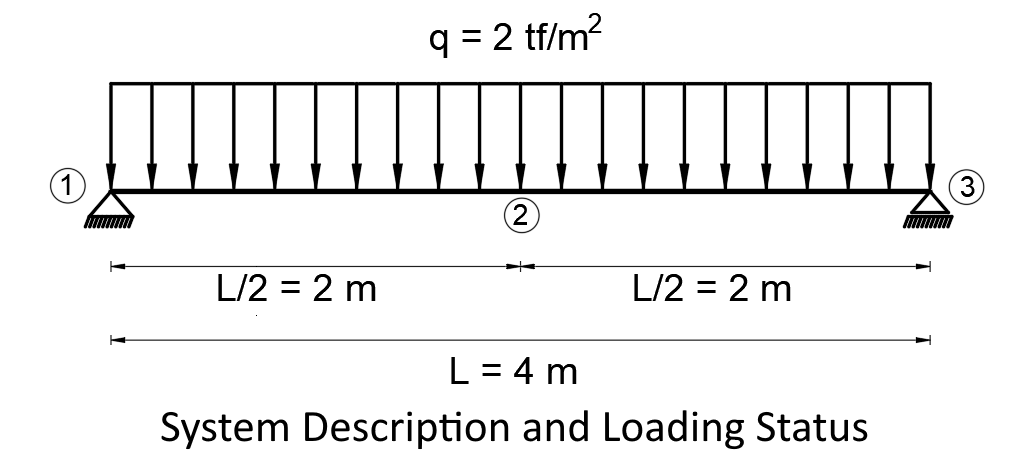
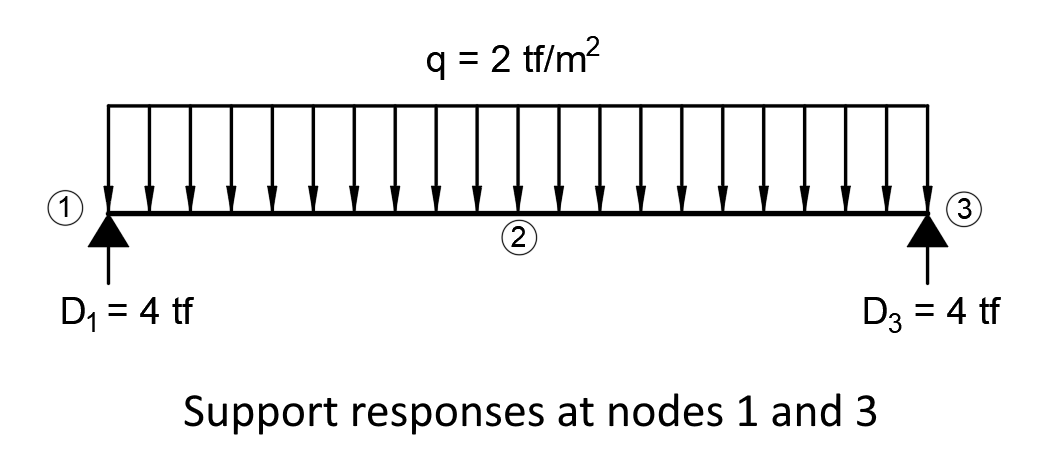
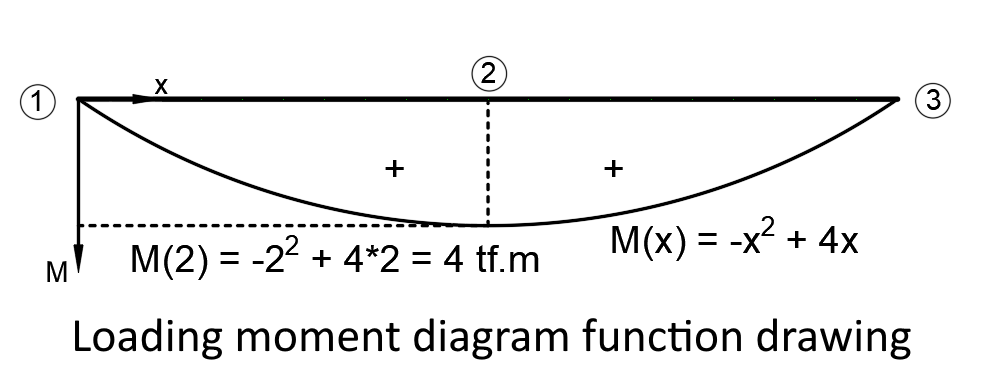
q: Distributed load D₁ , D₃ : Support responses M(2): 2 DN moment value L: Element length

M(x): Moment function ΣM_1,dn : Total moment with respect to 1 DN.
ΣD: Total balance

Moment Function :

Step 3: Multiplying the M and M' Moment Functions in the Previous Steps and Getting the Integral

Integral for 1-2 Bar

Integral for 2-3 Bar

Deformation of node 2 = 0.107m

Next Topic

2D Frame I

Related Topics