Torsional Strength per ACI 318-19 with ideCAD (v12)

How does ideCAD calculate torsional strength according to ACI 318-19?

• Torsional strength will be calculated automatically in the next version (V12)

Notation

A_o = gross area enclosed by torsional shear flow path, in.²
A_oh = area enclosed by centerline of the outermost closed transverse torsional reinforcement, in.²
A_cp = area enclosed by outside perimeter of concrete cross section, in.²
A_g = gross area of concrete section, in²
A_l = total area of longitudinal reinforcement to resist torsion, in.²
A_l,min = minimum area of longitudinal reinforcement to resist torsion, in.²
A_t = area of one leg of a closed stirrup, hoop, or tie resisting torsion within spacing s, in.²
b_w = web width or diameter of circular section, in.
f_c^' = specified compressive strength of concrete, psi
(f_c^')^0.5 = square root of specified compressive strength of concrete, psi
f_pc = compressive stress in concrete, after allowance for all prestress losses, at centroid of cross section resisting externally applied loads or at junction of web and flange where the centroid lies within the flange, psi.
f_yt = specified yield strength of transverse reinforcement, psi
N_u = factored axial force normal to cross section occurring simultaneously with V_u or T_u; to be taken as positive for compression and negative for tension, lb
p_cp = outside perimeter of concrete cross section, in.
p_h = perimeter of centerline of outermost closed transverse torsional reinforcement, in.
s = center-to-center spacing of items, such as longitudinal reinforcement, transverse reinforcement, tendons, or anchors, in.
T_cr = cracking torsional moment, in.-lb
T_th = threshold torsional moment, in.-lb
T_n = nominal torsional moment strength, in.-lb
T_u = factored torsional moment at section, in.-lb
V_u = factored shear force at section, lb
ϕ = strength reduction factor
λ = modification factor to reflect the reduced mechanical properties of lightweight concrete relative to normal-weight concrete of the same compressive strength

Torsional design is made with the reinforcement requirement determined by comparing the factored torsional moment T_u value with the threshold torsion T_th and cracking torsion T_cr values.

• Torsional effects can be neglected if the factored torsional moment at section T_u is less than threshold torsion multiplied by strength reduction factor ϕT_th (T_u<ϕT_th). Torsional moments that do not exceed the threshold torsion T_th will not cause a structurally significant reduction in either flexural or shear strength and can be ignored.

• If T_u ≥ ϕT_cr it is assumed that closed stirrups, longitudinal bars, and compression diagonals provide the torsional resistance. Therefore, the reinforced concrete member is designed to resist T_u.

• If ϕT_cr > T_u ≥ ϕT_th, only minimum tension rebar needs to be provided ACI 9.6.4.

Threshold Torsion

Threshold torsion T_th is calculated in accordance with ACI Table 22.7.4.1(a) and 22.7.4.1(b). Factored axial force, N_u is positive for compression and negative for tension. The modification factor λ, given for concrete class specified in ACI Table 19.2.4.2, and equals 1 for normal-weight concrete.

Threshold torsion T_th is calculated for nonprestressed according to the equation given below.

Cracking Torsion

Cracking torsion T_cr is calculated in accordance with ACI Table 22.7.5.1. Factored axial force N_u is positive for compression and negative for tension. The modification factor λ, given for concrete class specified in ACI Table 19.2.4.2, equals 1 for normal-weight concrete.

The maximum value of the (f_c^')^0.5 [or :fcuss:] used to calculate T_cr and T_th is 100 psi.

Torsional strength

For nonprestressed reinforced concrete members, nominal torsional moment strength T_n is the minimum value of the given equations below.

A_o is determined by using analysis results, θ is between 30 degrees and 60 degrees; A_t is the area of one leg of a closed stirrup resisting torsion; A_l is the longitudinal torsional reinforcement area; and p_h is the perimeter of the centerline of the outermost closed stirrup.

• If T_u < ϕT_th, torsional effects are ignored.

• If ϕT_cr > T_u ≥ ϕT_th, only minimum torsional reinforcement needs to be provided given below;

Minimum transverse reinforcement (A_v + 2A_t)_min / s

the minimum area of longitudinal reinforcement A_l,min

• If T_u > ϕT_cr total area of longitudinal reinforcement to resist, torsion A_l is calculated bu using nominal torsional moment strength T_n. In addition, minimum reinforcement requirements are checked.

There is an upper limit of the combination of V_u and T_u. Cross-sectional dimensions should be satisfied the ACI Eq. (22.7.7.1a);

For solid sections,

Special Section Properties for Torsional Strength

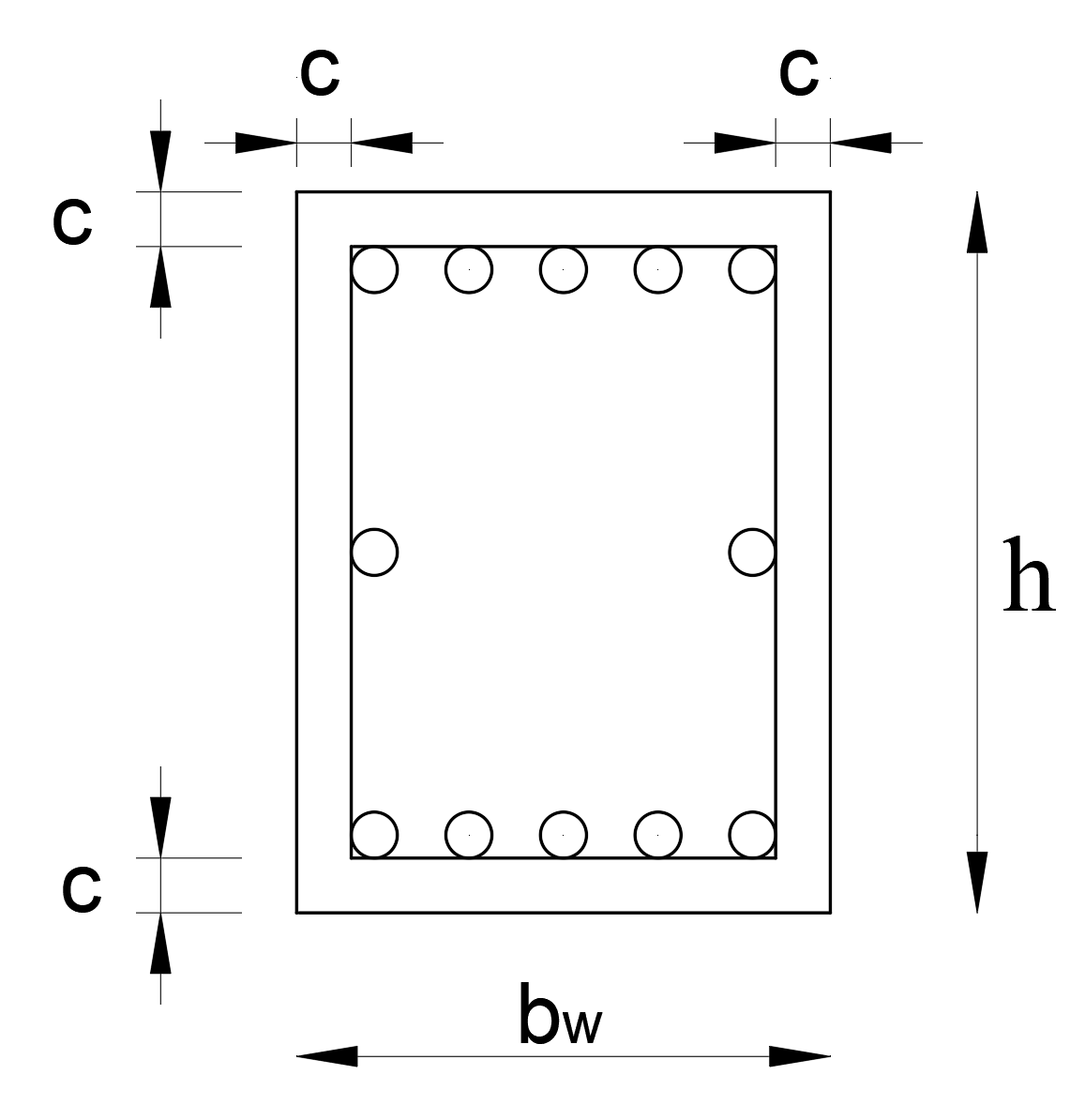
A_cp = b_wh

A_oh = (b_w − 2c)(h − 2c)

A_o = 0.85 A_oh

p_cp = 2b_w + 2h

p_h = 2(b_w − 2c) + 2(h − 2c)

For the calculation of Torsional strength, it is assumed that the unit of (f_c^')^0.5 [or :fcuss:] is psi. If these values are to be calculated in SI-metric or mks-metric units, the (f_c^')^0.5 [or :fcuss:] value is changed accordingly.

Next Topic

Reinforcement Details per ACI 318-19 §25

Related Topics

• Flexural Strength per ACI 318-19 with ideCAD

• Axial strength or Combined Flexural and Axial Strength per ACI 318-19 with ideCAD

• One-Way Shear Strength per ACI 318-19 with ideCAD

• Two-Way Shear Strength per ACI 318-19 with ideCAD

• Reinforced Concrete Column Design per ACI 318-19 §10, §18