15.5.4.1
In linear performance analysis, the total displaced axis rotation θ k value obtained at the nodal point (end) of each element is used to determine the current structure performance . The displaced axis rotation is obtained using the Mode Combination Method using the rotation value of the node and the relative offset of the element between two nodes.
The unit deformation and plastic rotation demands of the element sections are calculated automatically as a result of the Earthquake Calculation with the Mode Combination Method made according to TBDY 4.8.2 .
Displaced axis rotation θ k is automatically calculated according to EK 15A .
ICONS
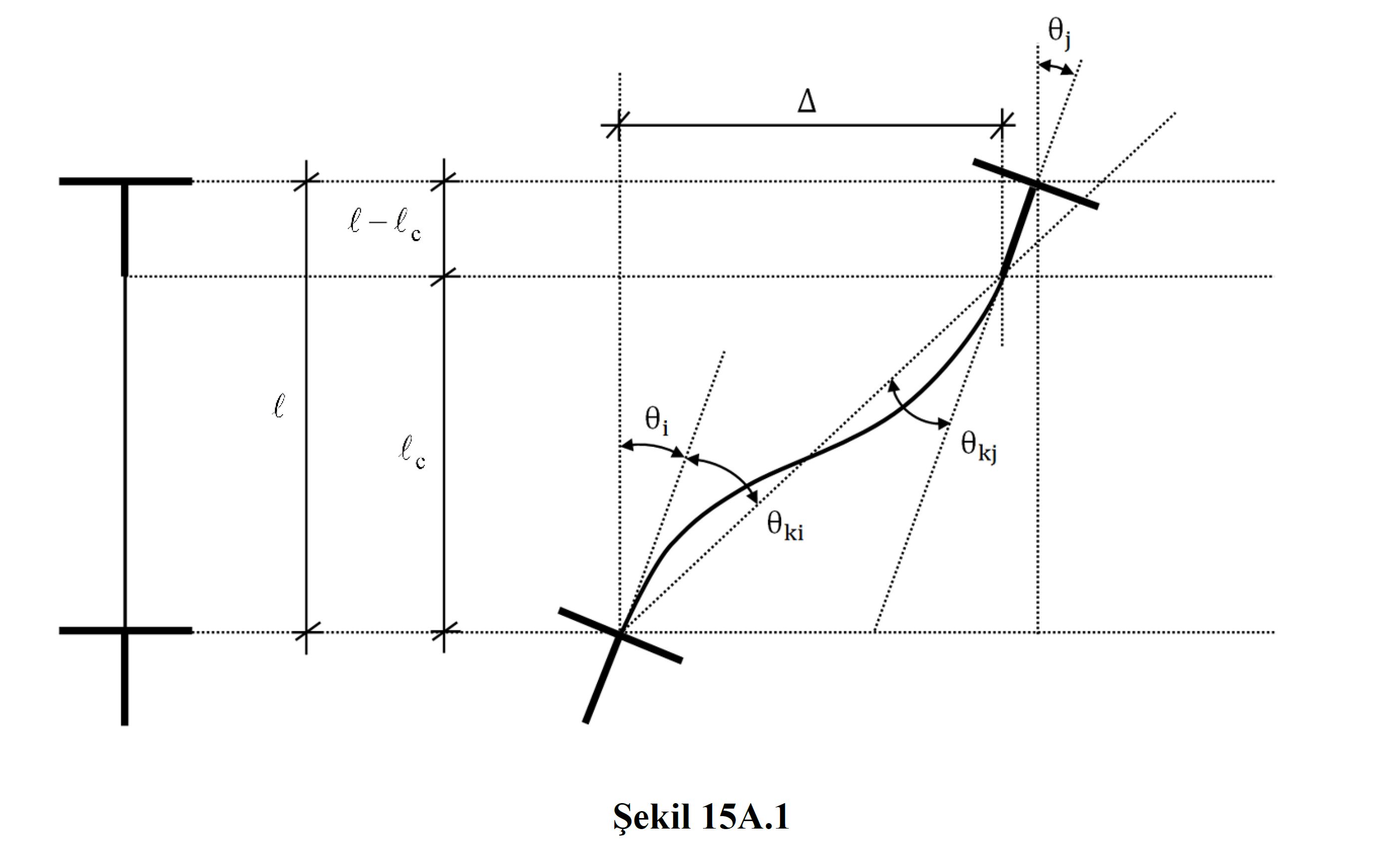
l = Total length of element
l c = Element net span
Δ = Displacementbetween element nodes
θ k = Displaced axis rotation
θ ki = displaced axis rotation at end i
θ kj = displaced axis rotation at end j
θ i = i joint rotation
θ j = j node rotation
The unit deformation and plastic rotation demands of the element sections are obtained as a result of the Earthquake Calculation with the Mode Combination Method made according to Section 4.8.2 of TBDY . As a result of this calculation, the total displaced axis rotation obtained at the node (end) of each element is determined using θ k .
At the end of a bending element i of the pivot axis likelihood disposition θ in Eq. (15A.1) included with.
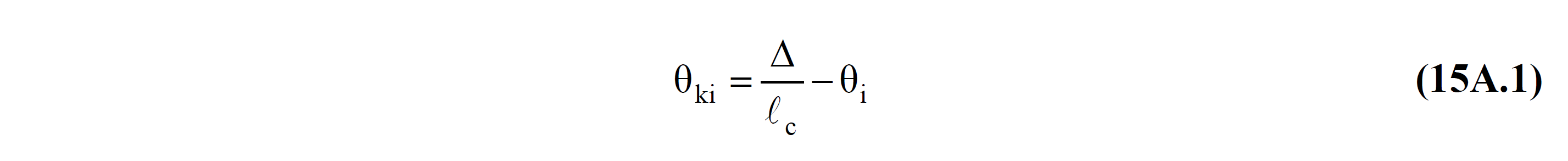
In this equation Δ is the relative displacement (displacement) between two joints, l c means the element net span. θ i is the rotation value of the joint point i obtained as a result of the Earthquake Calculation with the Mode Combination Method . Figure 15A.1 shows the rotation of joint i and j θ i and θ j and displaced axis rotation θ ki and θ kj . The detailed explanation is at Definition of Displaced Axis Rotations for Column, Shearwall and Beam Elements .
Next Topic
Related Topics
