Instantaneous and Time Dependent Deflection Example 2

In this example, Dead loads are increased, so that the bending moment value of the element is greater than the cracking moment value of the element.

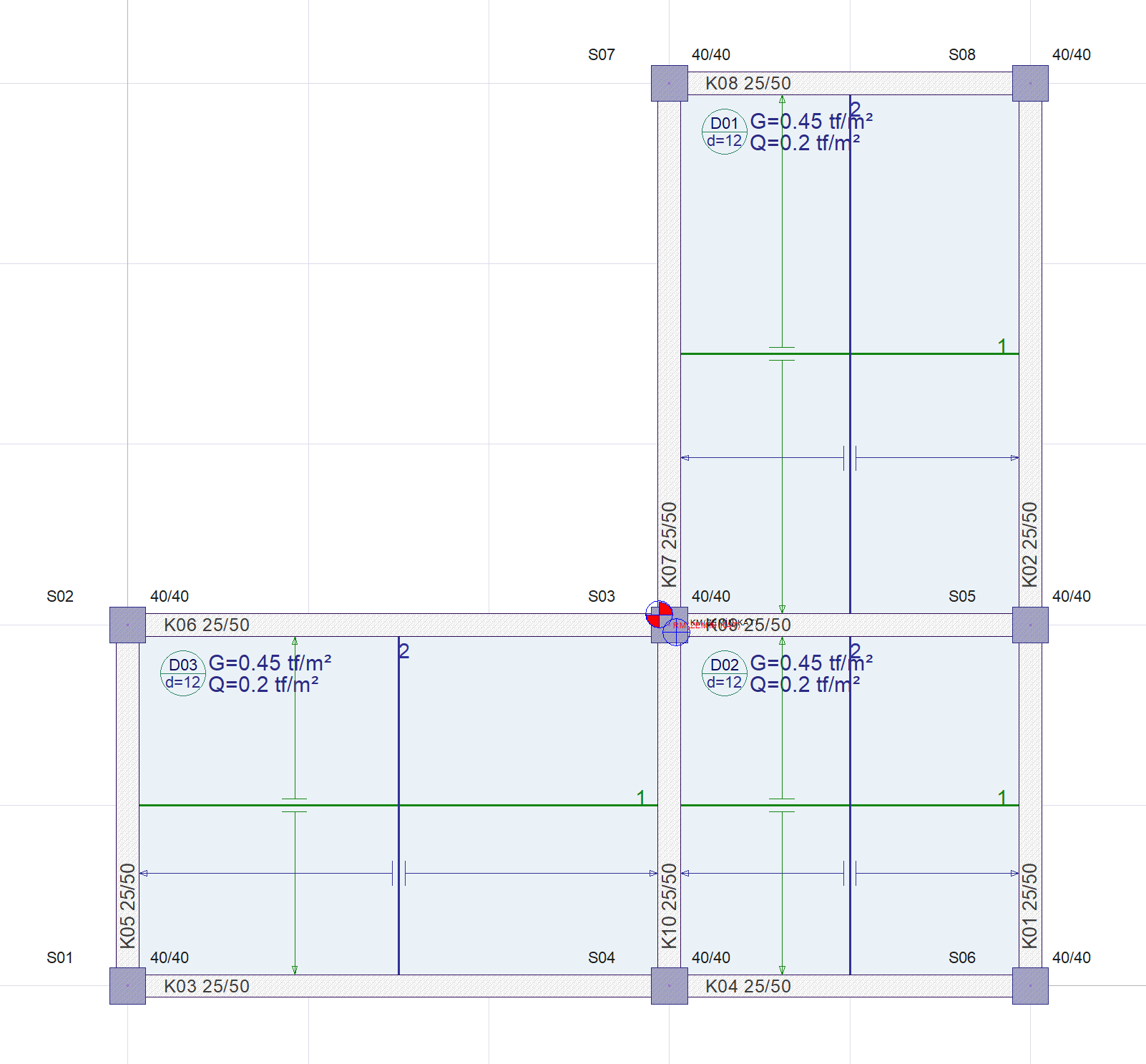
In the structure whose plan view is given in the image below, the instantaneous deflection calculation will be made for the K06 beam and compared with the ideCAD results. For the K06 beam, instantaneous deflection under the effect of live loads (Q) and instantaneous deflection and time-dependent deflection calculations for Dead Loads (G) will be made. The results will be compared with ideCAD v10 by calculating the total deflection from the deflections consisting of fixed and live loads.

Important Note: Deflection in reinforced concrete elements is calculated with Effective Moments of Inertia in ideCAD software . Then, taking into account these effective moments of inertia, a new analysis is made for the deflection control of the structure only. However, in this example, approximate formulas will be used to calculate the beam deflection calculation easier by hand and only deformations due to bending will be considered. In ideCAD software, the deformation effects of all internal forces are taken into account. For this reason, manual calculation and ideCAD results may differ slightly.

Proje Dosyası

Instantaneous and Time Dependent Deflection Example 2.rar

K06 Beam Section Properties

• Modulus of elasticity of concrete, E_c = 30250 MPa

• Modulus of elasticity of Reinforcement E_s = 200000 MPa

• Design tensile strength of concrete, f_ctd = 1.167 MPa

• T-beam width 69.9 cm

• Span length of beam l_n = 5.60 m

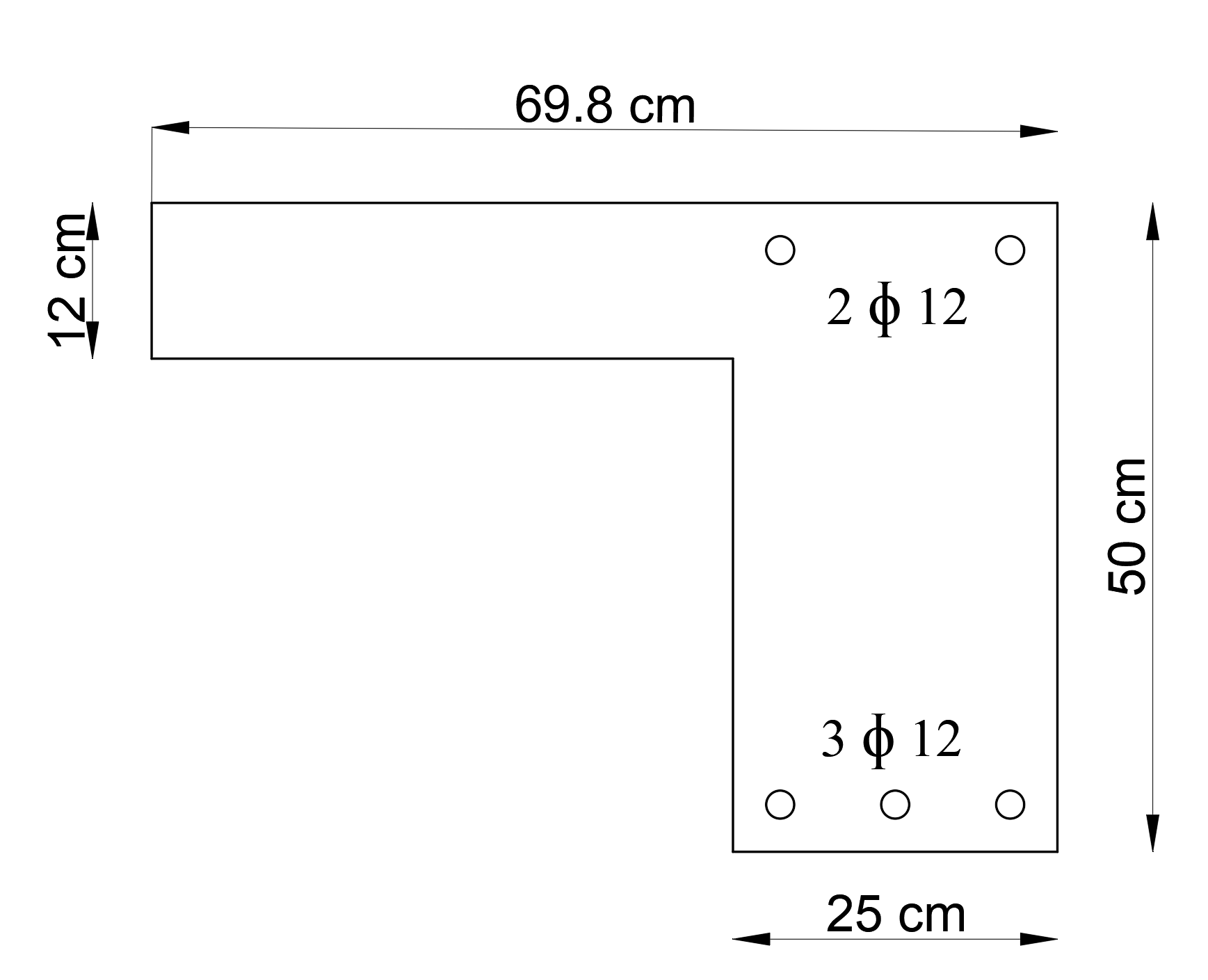
Calculation of Section Center of Gravity and Gross Concrete Section Moment of Inertia

Moment of inertia of gross concrete section I_c, is calculated about controidal axis. Therefore, the axis of the center of gravity of the section, distance from centroidal axis of gross section, neglecting reinforcement, to top surface and distance from centroidal axis of gross section, neglecting reinforcement, to bottom surface of the section should be calculated.

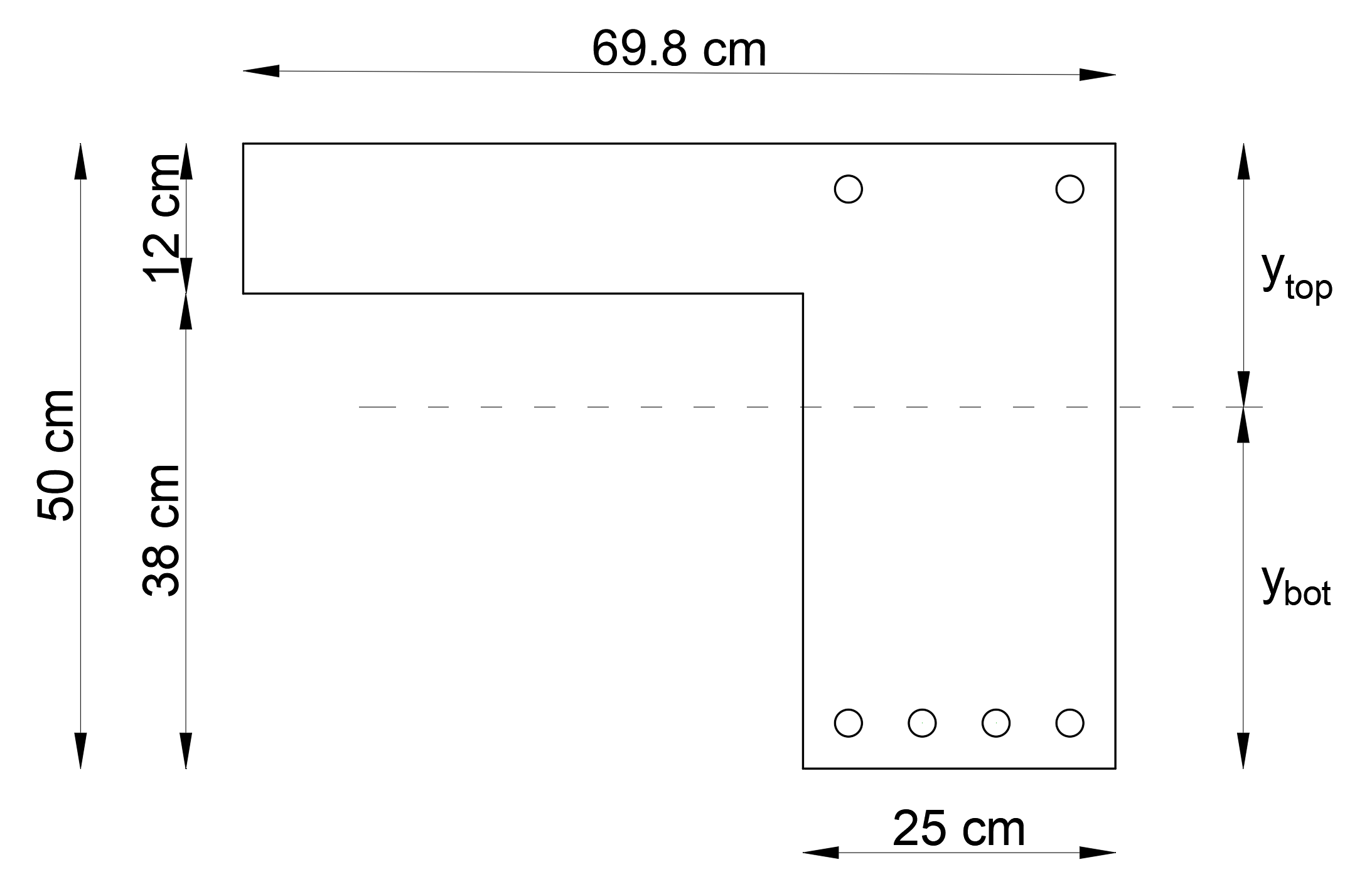
y_top : distance from centroidal axis of gross section, neglecting reinforcement, to top surface

y_bot : distance from centroidal axis of gross section, neglecting reinforcement, to bottom surface

Moment of inertia of gross concrete section about controidal axis, I_c is calculated as follows

Section Cracking Control

The span, right and left moment values (M_max) for the K06 beam are compared with the cracking moment M_cr of the member.
If M_max ≤ M_cr moment of inertia of gross concrete section I_c is used for deflection.
If M_max > M_cr Effective moment of inertia I_ef is used for deflection.

M_cr is calculated in accordance with TS500 13.2. y is distance from centroidal axis of gross section, neglecting reinforcement, to tension surface. For this reason, M_cr values should be calculated separately both in the span and in the end regions.

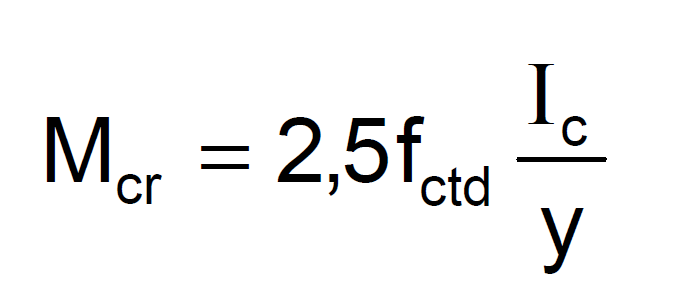
For the end region, the bending cracking moment M_cr is calculated as follows.

For the span region, the bending cracking moment M _cr is calculated as follows.

Beam Cracking Control Under Constant Load (G) and Live Load (Q)

The moment diagram of the K06 beam for the G+Q loading combination is shown below.

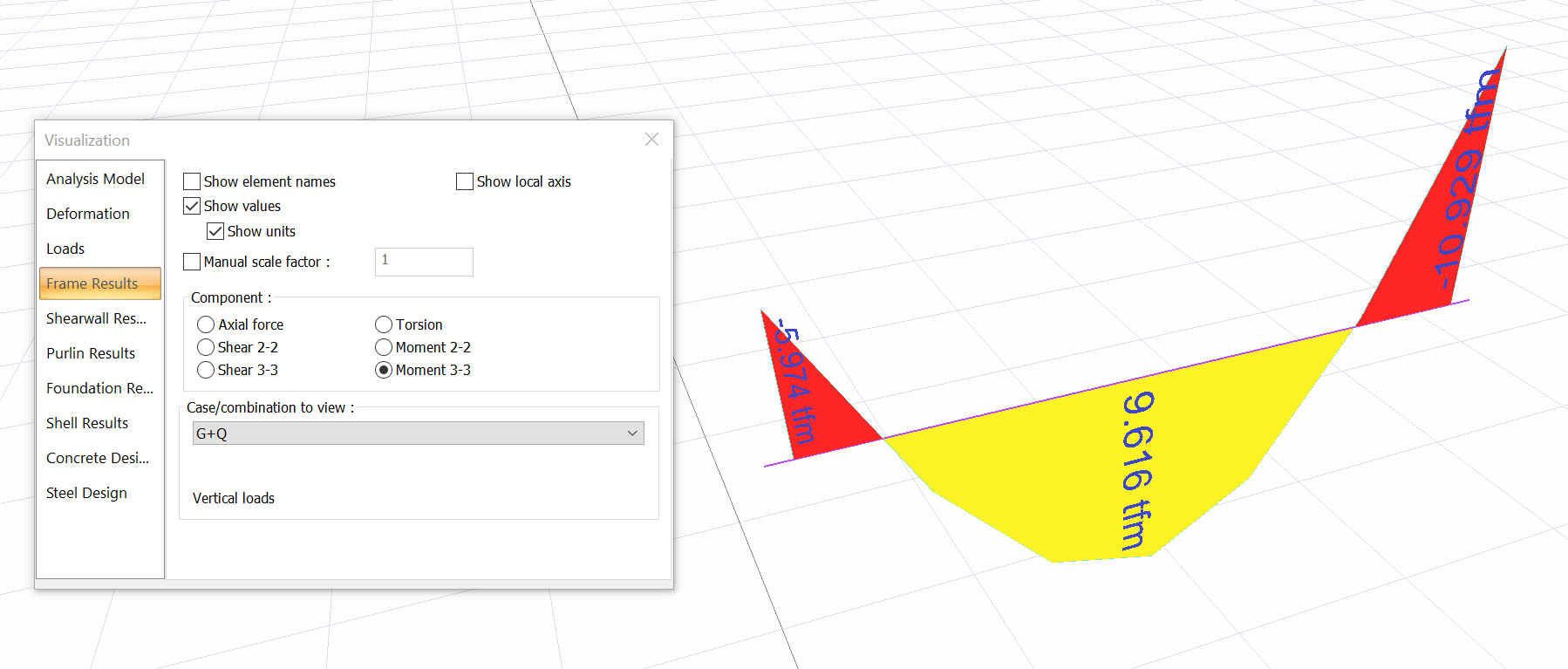
At the left end region, the bending cracking moment is calculated as M_cr = 6,208 tfm.

Since M_cr = 6.208 tfm > M_max-left = 5.974 tfm, no cracking occurred at the left end region. For this reason, Moment of inertia of gross concrete section I_c value is used in the deflection calculation.

At the right end region, the bending cracking moment is calculated as M_cr = 6,208 tfm.

Since M_cr = 6.208 tfm ≤ M_max-right = 10.929 tfm , cracking occurred at the right end region. For this reason, Effective moment of inertia I_eff value is used for calculation of deflection.

In the span region, the bending cracking moment is calculated as M_cr = 3.898 tfm.

Since M_cr = 6.208 tfm ≤ M_max-span = 10.929 tfm , cracking occurred at the span. For this reason, Effective moment of inertia I_eff value is used for calculation of deflection.

Moment of Inertia of Cracked Section I_cr ve Effective Moment of Inertia I_eff Calculation for Span Region

In the calculation of the moment of inertia of the cracked section, the compression zone of the section and the reinforcement placement are taken into account. The figure below shows the span region for the opening region and the concrete compression region and reinforcement placement.

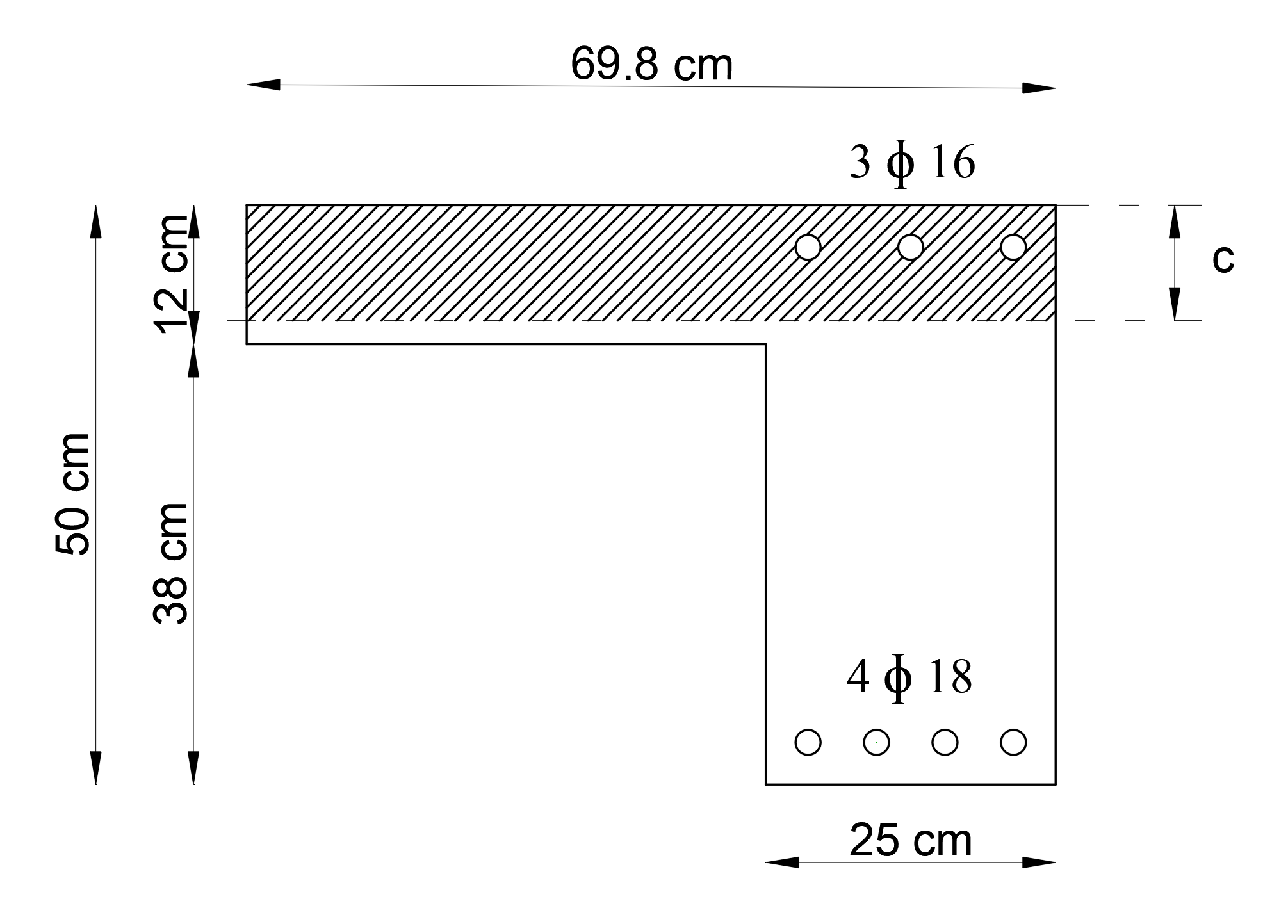
ρ is tension reinforcement ratio, ρ' is compression reinforcement ratio;, d is distance from extreme compression fiber to centroid of longitudinal tension reinforcement, and d' is concrete cover. olmak üzere, The location of the neutral axis k_c and the height of the neutral axis c values incracked reinforced section are found as follows.

Moment of inertia of cracked section transformed to concrete I_cr is calculated as follows for span region.

Effective moment of inertia I_eff is calculated as follows for span region.

Moment of Inertia of Cracked Section I_cr ve Effective Moment of Inertia I_eff Calculation for Right End Region

In the calculation of the moment of inertia of the cracked section, the compression zone of the section and the reinforcement placement are taken into account. The figure below shows the right end region for the opening region and the concrete compression region and reinforcement placement.

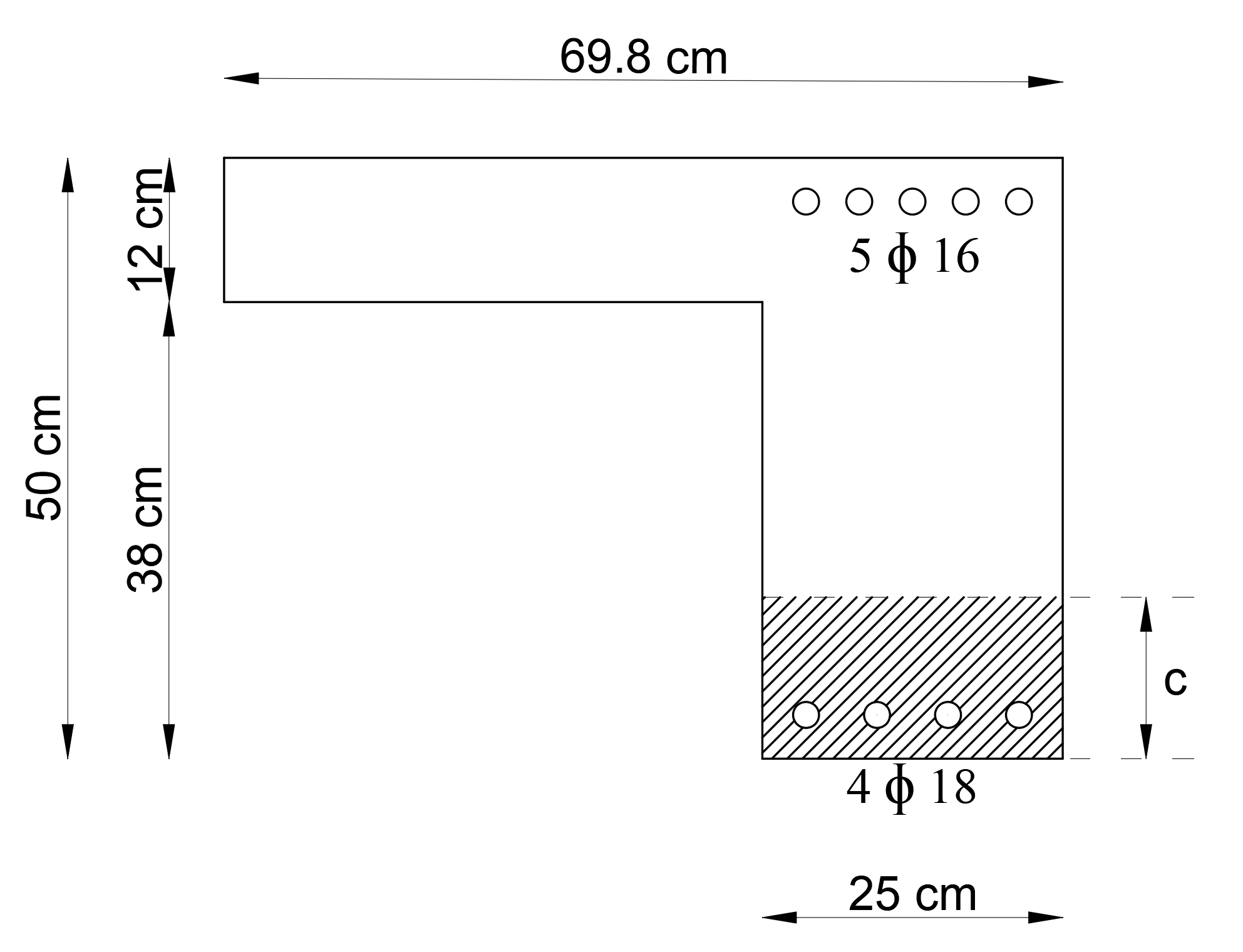
ρ is tension reinforcement ratio, ρ' is compression reinforcement ratio;, d is distance from extreme compression fiber to centroid of longitudinal tension reinforcement, and d' is concrete cover. olmak üzere, The location of the neutral axis k_c and the height of the neutral axis c values incracked reinforced section are found as follows.

Moment of inertia of cracked section transformed to concrete I_cr is calculated as follows for left end region.

Effective moment of inertia I_eff is calculated as follows for left end region.

Average Effective Moment of Inertia

The Average effective moment of inertia I_eff-ave of K06 beam is calculated by the effective moment of inertia I_eff values in left end, span and right end region. The deflection is calculated with Average Effective Moment of Inertia I_eff-ave value.

Instantaneous Deflection Under Live Load (Q) Effects

The moment diagram of the K06 beam for the Live Load (Q) effects is shown below.

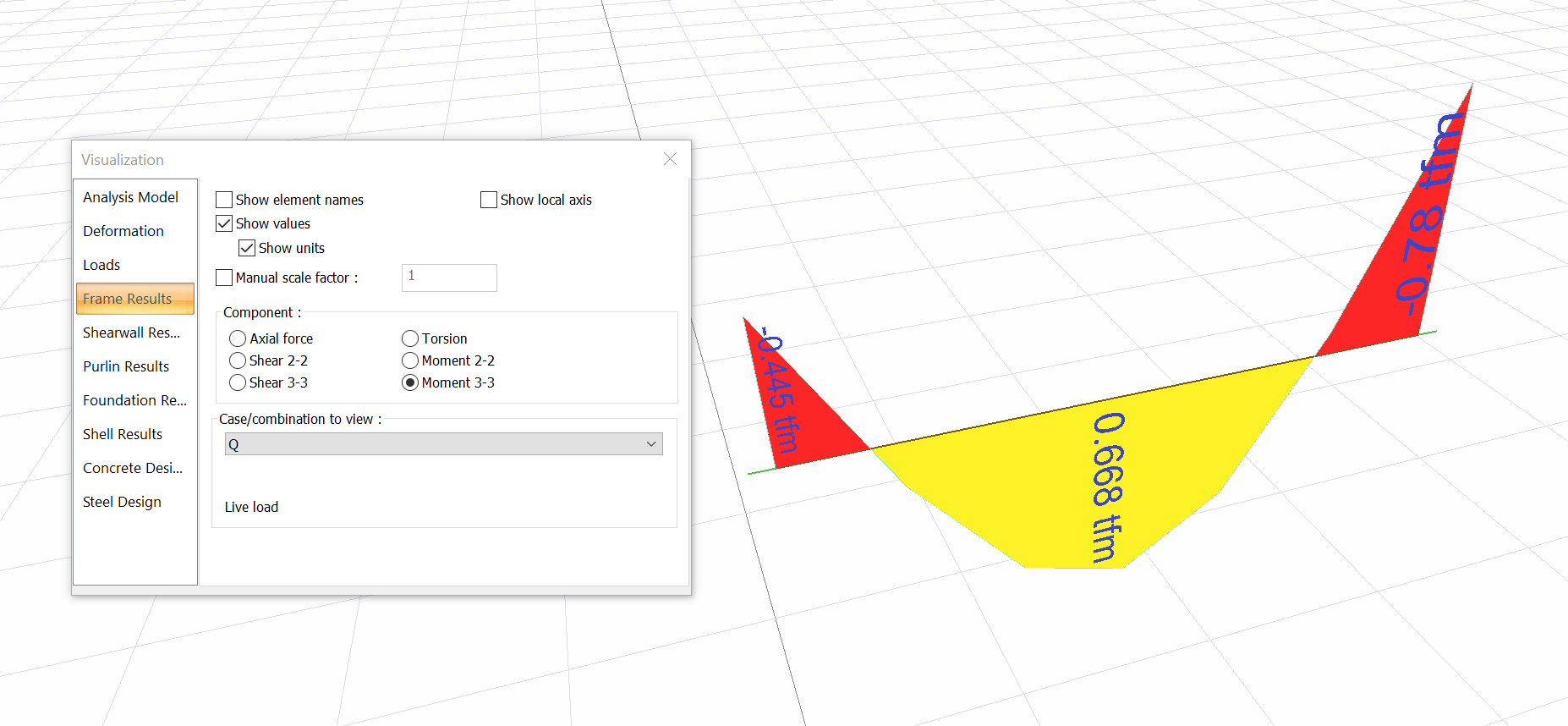
Instantaneous deflection due to live loads, δ_iQ

Deflection control;
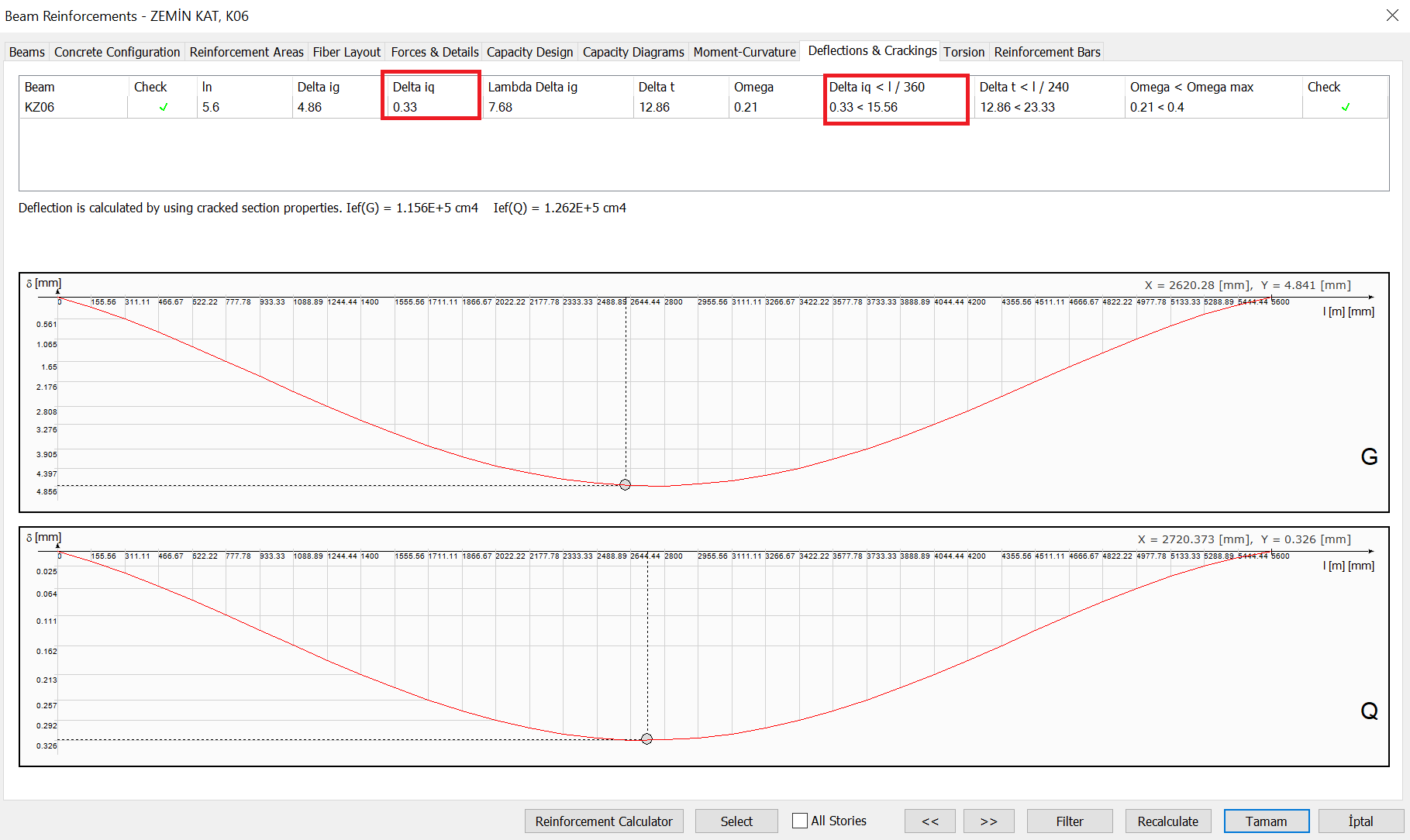
δ_iQ = 0.30 mm < l_n/360 =5600/360= 15.55 mm

The deflection results of the K06 beam under the Live Load (Q) effect in the Beam Reinforcement window are shown below.

Instantaneous Deflection Under Dead Load (G) Effects

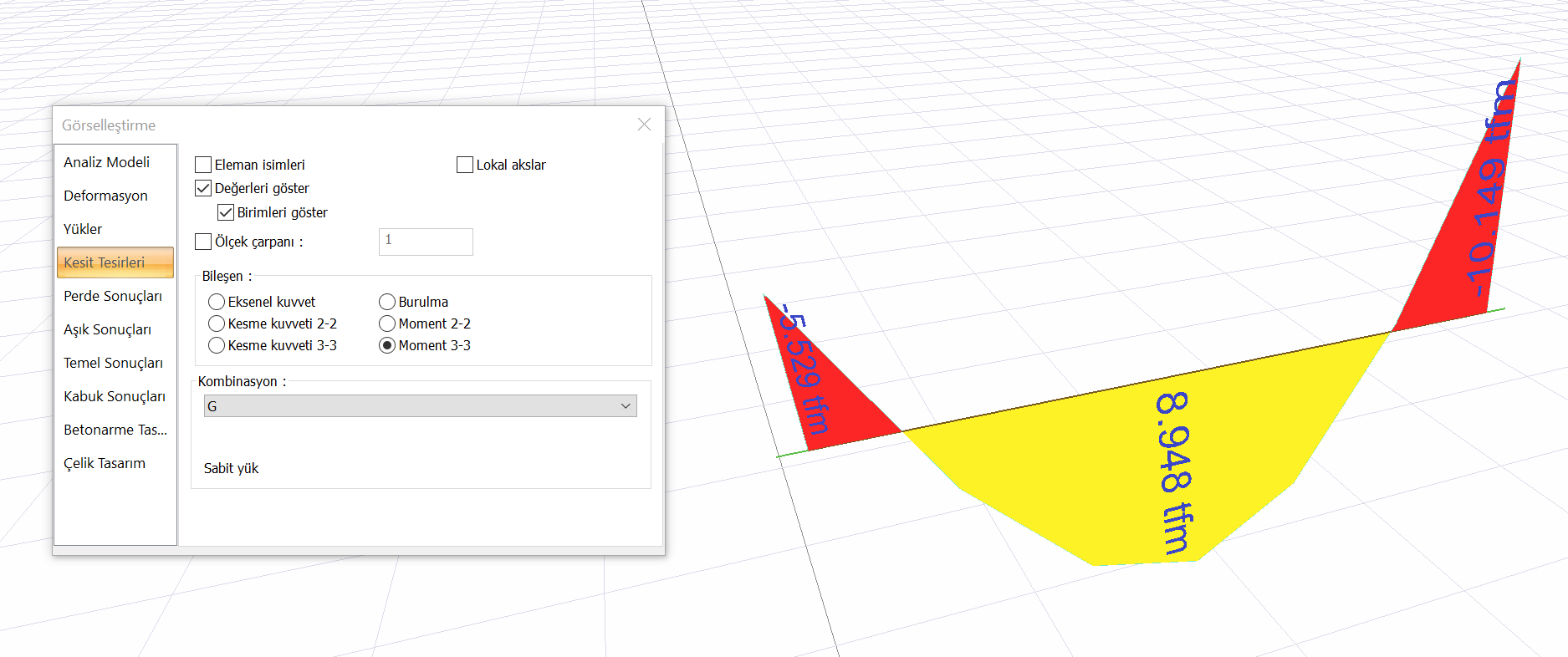
The moment diagram of the K06 beam for the DEad Load (G) effects is shown below.

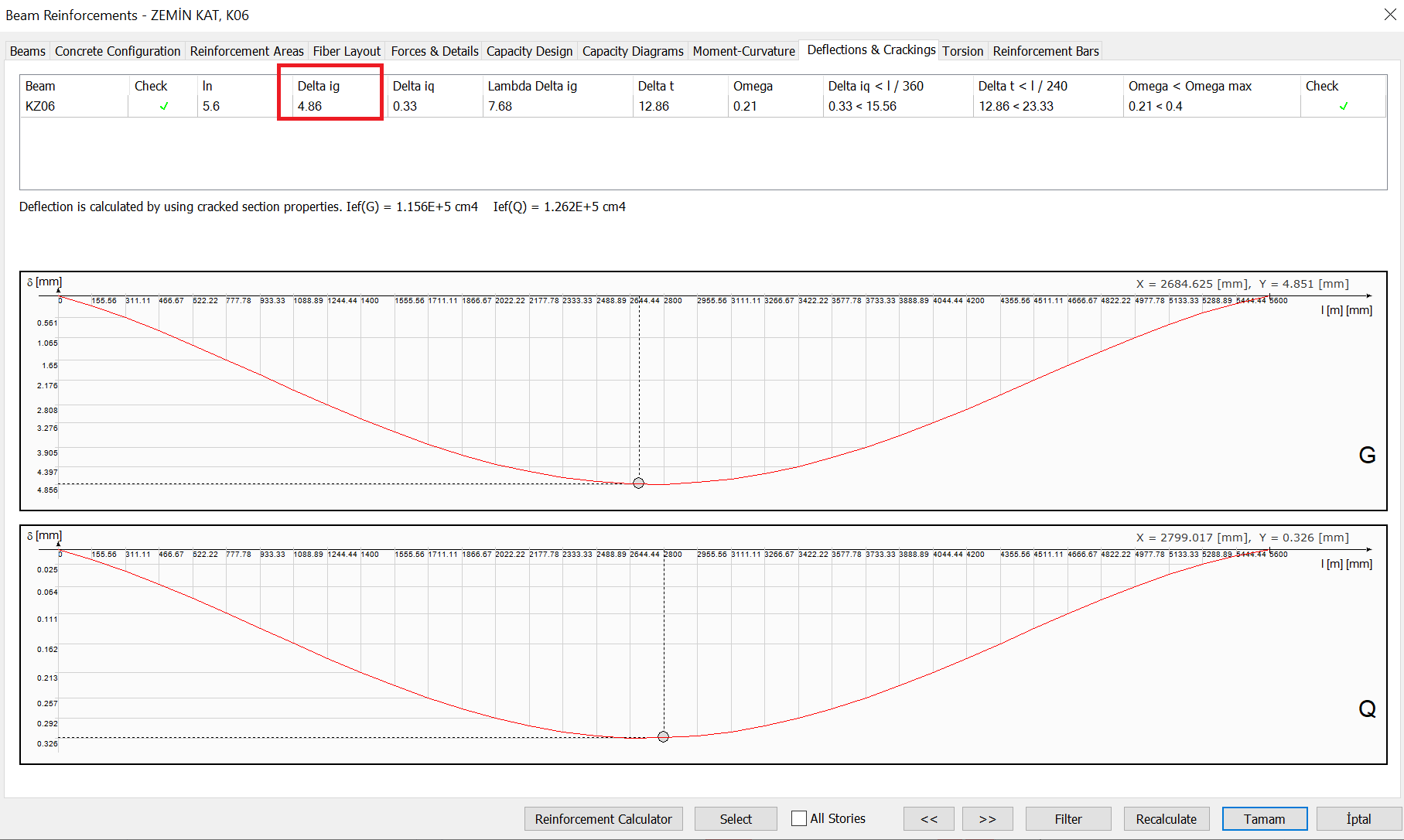
Instantaneous deflection due to dead loads, δ_iG

The deflection results of the K06 beam under the Dead Load (G) effect in the Beam Reinforcement window are shown below.

Time Dependent Deflection

Total deflection calculation and permanent deflection coefficient formulas are shown below.

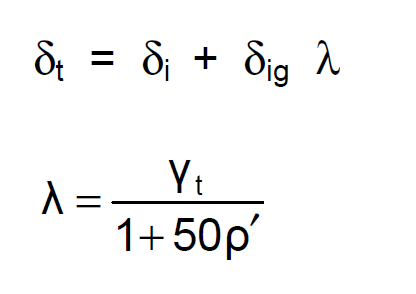
Permanent deflection multiplier γ_t is taken as 2.0 based on 5 years or more loading time in accordance with Table 13.2.

A_s' is area of the compression reinforcement and ρ' Compression reinforcement ratio;

When calculating the total deflection δ_t, the instantaneous deflection δ_iQ consisting of live loads, the instantaneous deflection δ_iG consisting of dead loads and the time-dependent deflection δ_iGλ are added. In this situation total deflection δ_t is calculated as follows.

Deflection control;
δ_t = 10.82 mm < l_n/240 =5600/360= 23.33 mm

The total deflection results of the K06 beam in the Beam Reinforcement window under the effect of Dead and Live loads are shown below.

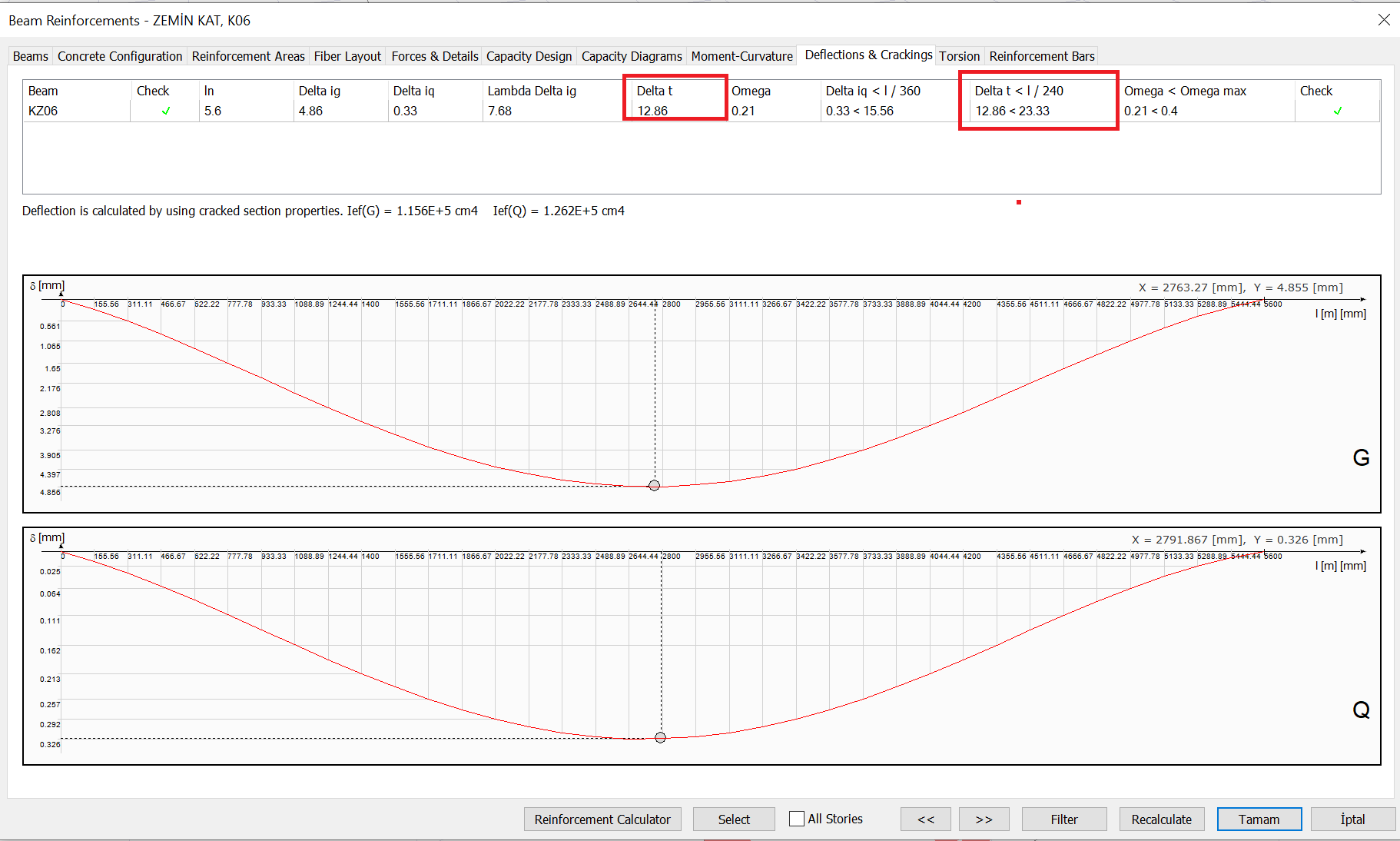
The results calculated above can also be checked in the Beam Deflections and Crackings Report .

Next Topic

Building Base and Building Height

Related Topics

• Instantaneous and Time Dependent Deflection Example 1

• Deflection Control

• Instantaneous Deflections (TS500)

• Time-Dependent Deflections (TS500)

• Deflection Limits (TS500)