Beam Flexural Design.
Beam flexural design strengths are calculated automatically.
Beam required strengths are calculated automatically.
International Design Codes
ACI 318-19 : Beam Flexural Design per ACI 318-19 with ideCAD
TSC 2018 :
Notation in ACI 318-19
As = area of nonprestressed longitudinal tension reinforcement, in2
Ag = gross area of concrete section, in2
α = depth of equivalent rectangular stress block, in.
bw = web width or diameter of circular section, in.
c = distance from extreme compression fiber to neutral axis, in.
Cc = concrete compressive force, lb
Cs = reinforcement tension force, lb
d = distance from extreme compression fiber to centroid of longitudinal tension reinforcement, in.
D = dead load
E = earthquake load
fc' = specified compressive strength of concrete, psi
fy = specified yield strength for nonprestressed reinforcement, psi
fyt = specified yield strength of transverse reinforcement, psi
L = live load
Lr = roof live load
Mn = nominal flexural strength at section, in.-lb
Mu = factored moment at section, in.-lb
Pu = factored axial force; to be taken as positive for compression and negative for tension, lb
R = rain load
S = snow load
U = strength of a member or cross section required to resist factored loads or related internal moments and forces in such combinations
Vn = nominal shear strength, lb
Vu = factored shear force at section, lb
W = wind load
ρ = ratio of As to bd
ϕ = strength reduction factor
The beam top and bottom flexural reinforcement is designed along the beam span.
Nominal flexural strength with zero compression is calculated as follows.
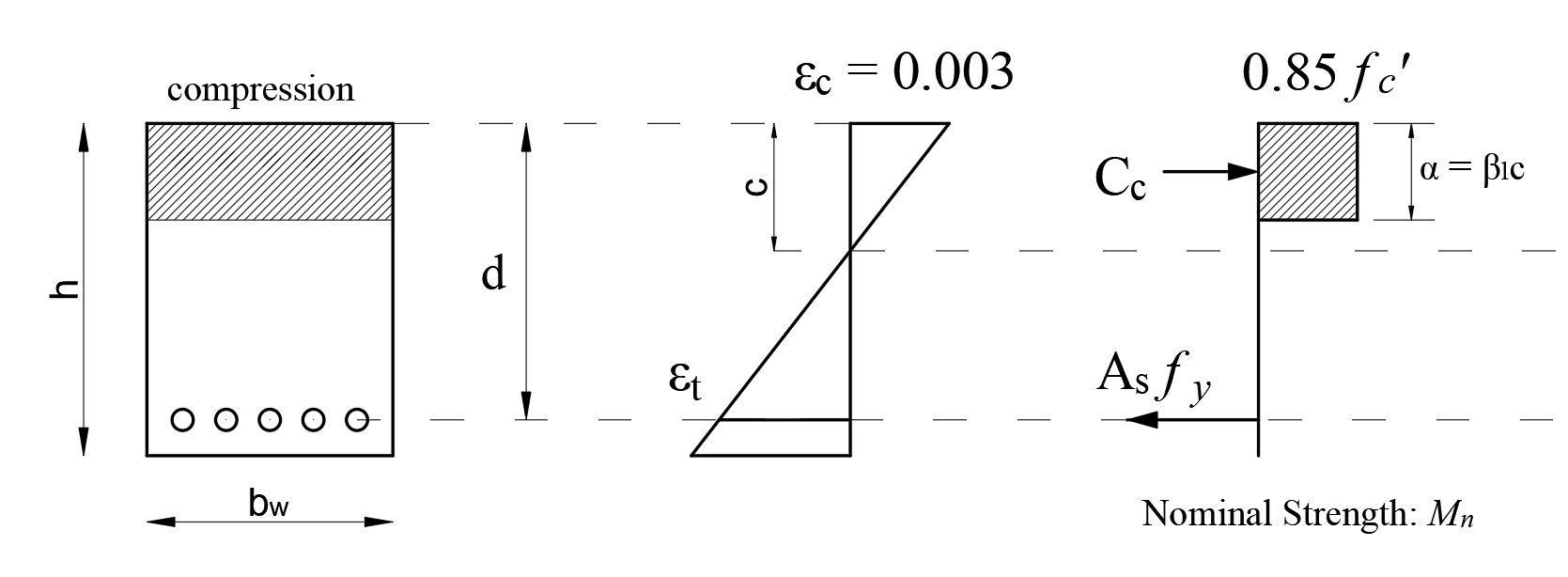
From the equation of equilibrium:
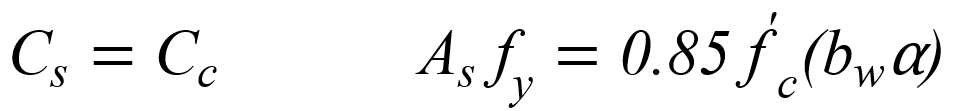
Nominal flexural strength Mn:

Next Topic
