Design of Steel Members for Tension per AISC 360-16 §D

How does ideCAD calculate steel members' tensile strength according to AISC 360-16?

• The tensile strength of steel elements is calculated automatically according to AISC 360-16.

• Limit states of tensile yielding are in the gross section, tensile rupture is in the net section, and block shear is controlled automatically according to AISC 360-16.

Symbols

A_g : Cross-section area without loss
A_e : Effective net cross-sectional area
A_n : Net cross-section area
A_gv : Area without loss under shear stress
A_nv : Net area under shear stress
A_nt : Net area under tensile stress
F_y : Structural steel characteristic yield stress
F_u : Structural steel characteristic tensile strength
K : Twisting length coefficient
L : Element length between supported points
i : Radius of inertia
U : Stress irregularity effect coefficient
U_bs : A coefficient considering the spread of tensile stresses
T_n : Design tensile strength

Tensile Strength of the Steel Elements

• Tension members are structural elements that transmit the axial tensile forces. If tension elements are used together with bolted joints, yield stress will be reached earlier in the areas where bolt holes are located. This situation will affect the strength determined by using the load-displacement curve.

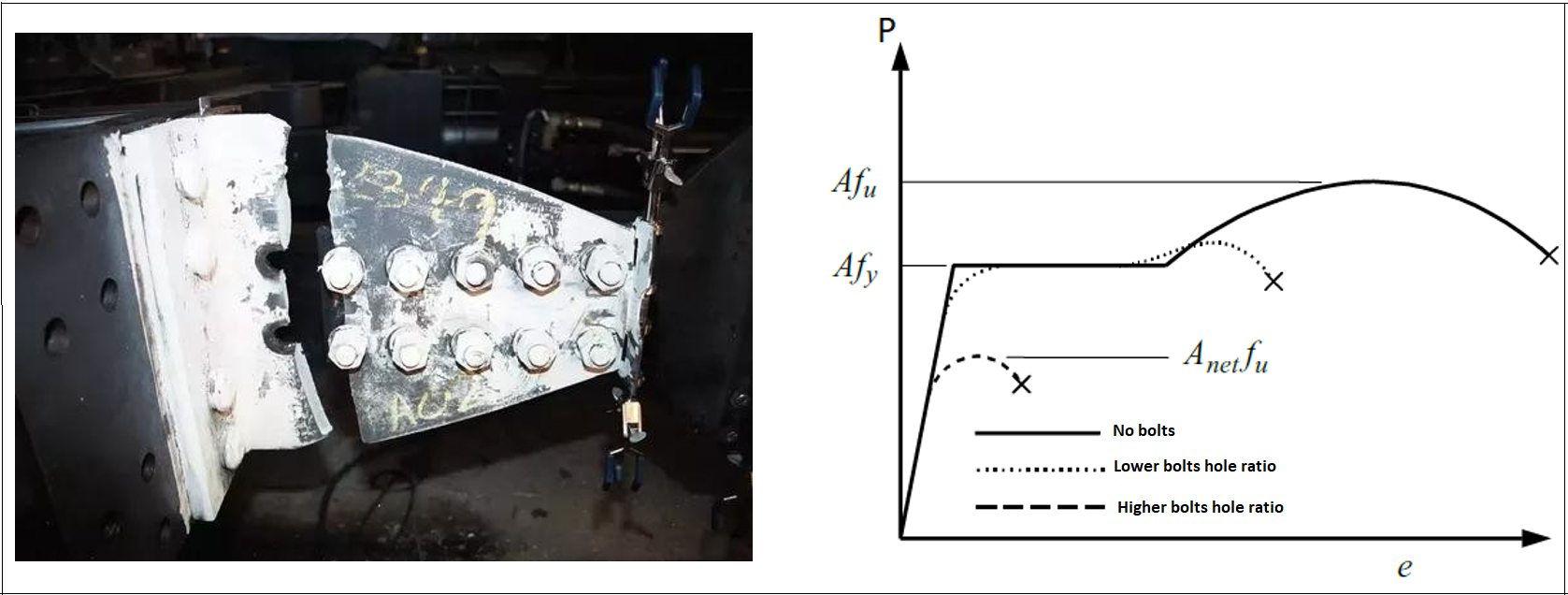
• In bolted and welded joints of tension members, the cross-sectional area operating in load transfer is not equal to the entire cross-section area due to the uneven distribution of the load.

• Since the L and U sections are used, especially in the corners not connected with bolts or welds, a certain region is called an effective area in load distribution. The consequence of this partial connection is that the connected element becomes overloaded, and the unconnected part is not fully stressed. Due to this phenomenon called the 'Shear Lag' effect, an effective net area is used in the design.

• Three different areas are used in the strength calculation of tension members:

  • Gross Area (A_g)

  • Net Area (A_n)

  • Effective Net Area (A_e)

Design with AISC 360-16

Three different collapse conditions in the elements are affected by the tensile force: Yielding Limit State, Rupture Limit State, and Block Shear Limit State.

The design tensile strength is taken as the minimum strength to be calculated according to the yield limit state, rupture limit state, and block shear limit state of the element under axial tensile force. Block shear limit state is an additional check for joints.

The tension element slenderness ratio should be controlled. In accordance with article D1 of the regulation, the slender ratio should be less than 300.

TENSILE STRENGTH

Yielding Limit State

• The design tensile strength, φ_tP_n, and the allowable tensile strength, P_n/Ω_t, of tension members, for yielding limit state in tensile members is calculated and determined by Equation D2-1.

Rupture Limit State

• The characteristic tensile strength, P_n, for rupture limit state in tensile members is determined by Equation D2-2 using the effective net cross-sectional area.

Block Shear Conditions

• The characteristic block shear strength is calculated by Equation 13.19, based on the yielding and rupture limit states along the R_n shear surface or surfaces and the rupture limit states along the vertical tensile surface. A_nt is the net area subject to tension. Where the tension stress is uniform U_bs=1; where the tension stress is nonuniform U_bs=0.5.

Next Topic

Design of Steel Members for Compression per AISC 360-16 §E